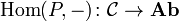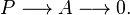Projective object
In category theory, the notion of a projective object generalizes the notion of a projective module.
An object P in a category C is projective if the hom functor
preserves epimorphisms. That is, every morphism f:P→X factors through every epi Y→X.
Let 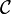 be an abelian category. In this context, an object
be an abelian category. In this context, an object 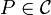 is called a projective object if
is called a projective object if
is an exact functor, where  is the category of abelian groups.
is the category of abelian groups.
The dual notion of a projective object is that of an injective object: An object  in an abelian category
in an abelian category 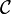 is injective if the
is injective if the 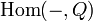 functor from
functor from 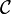 to
to  is exact.
is exact.
Enough projectives
Let  be an abelian category.
be an abelian category.  is said to have enough projectives if, for every object
is said to have enough projectives if, for every object  of
of  , there is a projective object
, there is a projective object  of
of  and an exact sequence
and an exact sequence
In other words, the map  is "epi", or an epimorphism.
is "epi", or an epimorphism.
Examples.
Let  be a ring with 1. Consider the category of left
be a ring with 1. Consider the category of left  -modules
-modules 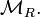
 is an abelian category. The projective objects in
is an abelian category. The projective objects in  are precisely the projective left R-modules. So
are precisely the projective left R-modules. So  is itself a projective object in
is itself a projective object in 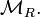 Dually, the injective objects in
Dually, the injective objects in  are exactly the injective left R-modules.
are exactly the injective left R-modules.
The category of left (right)  -modules also has enough projectives. This is true since, for every left (right)
-modules also has enough projectives. This is true since, for every left (right)  -module
-module  , we can take
, we can take  to be the free (and hence projective)
to be the free (and hence projective)  -module generated by a generating set
-module generated by a generating set  for
for  (we can in fact take
(we can in fact take  to be
to be  ). Then the canonical projection
). Then the canonical projection 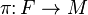 is the required surjection.
is the required surjection.
References
- Mitchell, Barry (1965), Theory of categories, Pure and applied mathematics 17, Academic Press, ISBN 978-0-124-99250-4, MR 0202787
This article incorporates material from Projective object on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License. This article incorporates material from Enough projectives on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.