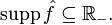Progressive function

From Wikipedia, the free encyclopedia

In mathematics, a progressive function ƒ ∈ L²(R) is a function whose Fourier transform is supported by positive frequencies only:

${\mathop {{\rm {supp}}}}{\hat {f}}\subseteq {\mathbb {R}}_{+}.$

It is called super regressive if and only if the time reversed function f(−t) is progressive, or equivalently, if

${\mathop {{\rm {supp}}}}{\hat {f}}\subseteq {\mathbb {R}}_{-}.$

The complex conjugate of a progressive function is regressive, and vice versa.

The space of progressive functions is sometimes denoted 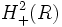$H_{+}^{2}(R)$ , which is known as the Hardy space of the upper half-plane. This is because a progressive function has the Fourier inversion formula

$f(t)=\int _{0}^{\infty }e^{{2\pi ist}}{\hat f}(s)\,ds$

and hence extends to a holomorphic function on the upper half-plane $\{t+iu:t,u\in R,u\geq 0\}$

by the formula

$f(t+iu)=\int _{0}^{\infty }e^{{2\pi is(t+iu)}}{\hat f}(s)\,ds=\int _{0}^{\infty }e^{{2\pi ist}}e^{{-2\pi su}}{\hat f}(s)\,ds.$

Conversely, every holomorphic function on the upper half-plane which is uniformly square-integrable on every horizontal line will arise in this manner.

Regressive functions are similarly associated with the Hardy space on the lower half-plane $\{t+iu:t,u\in R,u\leq 0\}$ .

This article incorporates material from progressive function on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.