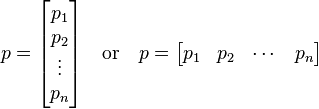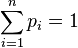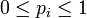Probability vector

From Wikipedia, the free encyclopedia

Stochastic vector redirects here. For the concept of a random vector, see Multivariate random variable.

In mathematics and statistics, a probability vector or stochastic vector is a vector with non-negative entries that add up to one.

The positions (indices) of a probability vector represent the possible outcomes of a discrete random variable, and the vector gives us the probability mass function of that random variable, which is the standard way of characterizing a discrete probability distribution.

Here are some examples of probability vectors. The vectors can be either columns or rows.

x_{0}={\begin{bmatrix}0.5\\0.25\\0.25\end{bmatrix}},\;x_{1}={\begin{bmatrix}0\\1\\0\end{bmatrix}},\;x_{2}={\begin{bmatrix}0.65&0.35\end{bmatrix}},\;x_{3}={\begin{bmatrix}0.3&0.5&0.07&0.1&0.03\end{bmatrix}}.

Writing out the vector components of a vector p as

p={\begin{bmatrix}p_{1}\\p_{2}\\\vdots \\p_{n}\end{bmatrix}}\quad {\text{or}}\quad p={\begin{bmatrix}p_{1}&p_{2}&\cdots &p_{n}\end{bmatrix}}

the vector components must sum to one:

\sum _{{i=1}}^{n}p_{i}=1

One also has the requirement that each individual component must have a probability between zero and one:

0\leq p_{i}\leq 1

for all i. These two requirements show that stochastic vectors have a geometric interpretation: A stochastic vector is a point on the "far face" of a standard orthogonal simplex. That is, a stochastic vector uniquely identifies a point on the face opposite of the orthogonal corner of the standard simplex.

Some Properties of n dimensional Probability Vectors

Probability vectors of dimension n are contained within an 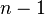n-1 dimensional unit hyperplane.
The mean of a probability vector is 1/n.
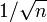The shortest probability vector has the value 1/n as each component of the vector, and has a length of 1/{\sqrt n}.
The longest probability vector has the value 1 in a single component and 0 in all others, and has a length of 1.
The shortest vector corresponds to maximum uncertainty, the longest to maximum certainty.
No two probability vectors in the n dimensional unit hypersphere are collinear unless they are identical.
The length of a probability vector is equal to {\sqrt {n\sigma ^{2}+1/n}}; where \sigma ^{2} is the variance of the elements of the probability vector.

See also

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.