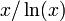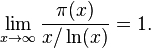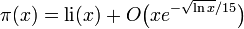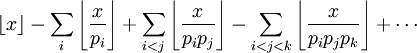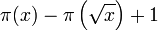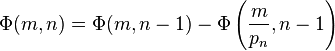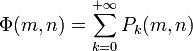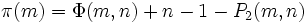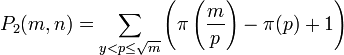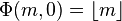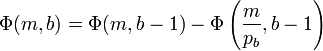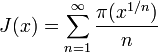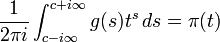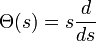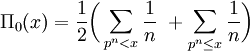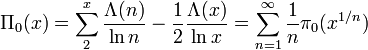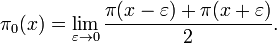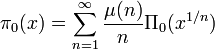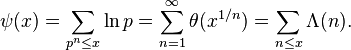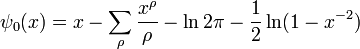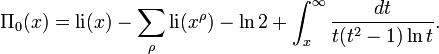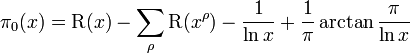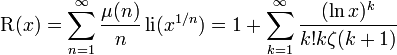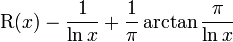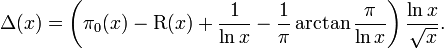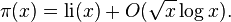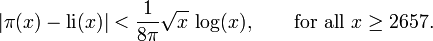Prime-counting function
In mathematics, the prime-counting function is the function counting the number of prime numbers less than or equal to some real number x.[1][2] It is denoted by 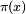 (this does not refer to the number π).
(this does not refer to the number π).

History
Of great interest in number theory is the growth rate of the prime-counting function.[3][4] It was conjectured in the end of the 18th century by Gauss and by Legendre to be approximately
in the sense that
This statement is the prime number theorem. An equivalent statement is
where li is the logarithmic integral function. The prime number theorem was first proved in 1896 by Jacques Hadamard and by Charles de la Vallée Poussin independently, using properties of the Riemann zeta function introduced by Riemann in 1859.
More precise estimates of  are now known; for example[citation needed]
are now known; for example[citation needed]
where the O is big O notation. For most values of  we are interested in (i.e., when
we are interested in (i.e., when  is not unreasonably large)
is not unreasonably large) 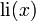 is greater than
is greater than  , but infinitely often the opposite is true. For a discussion of this, see Skewes' number.
, but infinitely often the opposite is true. For a discussion of this, see Skewes' number.
Proofs of the prime number theorem not using the zeta function or complex analysis were found around 1948 by Atle Selberg and by Paul Erdős (for the most part independently).[5]
Table of π(x), x / ln x, and li(x)
The table shows how the three functions π(x), x / ln x and li(x) compare at powers of 10. See also,[3][6][7] and.[8]
x π(x) π(x) − x / ln x li(x) − π(x) x / π(x) 10 4 −0.3 2.2 2.500 102 25 3.3 5.1 4.000 103 168 23 10 5.952 104 1,229 143 17 8.137 105 9,592 906 38 10.425 106 78,498 6,116 130 12.740 107 664,579 44,158 339 15.047 108 5,761,455 332,774 754 17.357 109 50,847,534 2,592,592 1,701 19.667 1010 455,052,511 20,758,029 3,104 21.975 1011 4,118,054,813 169,923,159 11,588 24.283 1012 37,607,912,018 1,416,705,193 38,263 26.590 1013 346,065,536,839 11,992,858,452 108,971 28.896 1014 3,204,941,750,802 102,838,308,636 314,890 31.202 1015 29,844,570,422,669 891,604,962,452 1,052,619 33.507 1016 279,238,341,033,925 7,804,289,844,393 3,214,632 35.812 1017 2,623,557,157,654,233 68,883,734,693,281 7,956,589 38.116 1018 24,739,954,287,740,860 612,483,070,893,536 21,949,555 40.420 1019 234,057,667,276,344,607 5,481,624,169,369,960 99,877,775 42.725 1020 2,220,819,602,560,918,840 49,347,193,044,659,701 222,744,644 45.028 1021 21,127,269,486,018,731,928 446,579,871,578,168,707 597,394,254 47.332 1022 201,467,286,689,315,906,290 4,060,704,006,019,620,994 1,932,355,208 49.636 1023 1,925,320,391,606,803,968,923 37,083,513,766,578,631,309 7,250,186,216 51.939 1024 18,435,599,767,349,200,867,866 339,996,354,713,708,049,069 17,146,907,278 54.243 1025 176,846,309,399,143,769,411,680 3,128,516,637,843,038,351,228 55,160,980,939 56.546

In the On-Line Encyclopedia of Integer Sequences, the π(x) column is sequence ![]() A006880, π(x) - x / ln x is sequence
A006880, π(x) - x / ln x is sequence ![]() A057835, and li(x) − π(x) is sequence
A057835, and li(x) − π(x) is sequence ![]() A057752. The value for π(1024) was originally computed by J. Buethe, J. Franke, A. Jost, and T. Kleinjung assuming the Riemann hypothesis.[9] It has since been verified unconditionally in a computation by D. J. Platt.[10]
A057752. The value for π(1024) was originally computed by J. Buethe, J. Franke, A. Jost, and T. Kleinjung assuming the Riemann hypothesis.[9] It has since been verified unconditionally in a computation by D. J. Platt.[10]
Algorithms for evaluating π(x)
A simple way to find 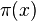 , if
, if  is not too large, is to use the sieve of Eratosthenes to produce the primes less than or equal to
is not too large, is to use the sieve of Eratosthenes to produce the primes less than or equal to  and then to count them.
and then to count them.
A more elaborate way of finding 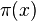 is due to Legendre: given
is due to Legendre: given  , if
, if 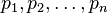 are distinct prime numbers, then the number of integers less than or equal to
are distinct prime numbers, then the number of integers less than or equal to  which are divisible by no
which are divisible by no  is
is
(where  denotes the floor function). This number is therefore equal to
denotes the floor function). This number is therefore equal to
when the numbers 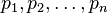 are the prime numbers less than or equal to the square root of
are the prime numbers less than or equal to the square root of  .
.
In a series of articles published between 1870 and 1885, Ernst Meissel described (and used) a practical combinatorial way of evaluating 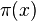 . Let
. Let  ,
, 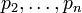 be the first
be the first  primes and denote by
primes and denote by 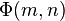 the number of natural numbers not greater than
the number of natural numbers not greater than  which are divisible by no
which are divisible by no  . Then
. Then
Given a natural number  , if
, if ![n=\pi \left({\sqrt[ {3}]{m}}\right)](/2014-wikipedia_en_all_02_2014/I/media/2/5/0/b/250b1776faaf8b1f19dbfc495f6bd0da.png) and if
and if 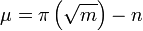 , then
, then
Using this approach, Meissel computed 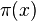 , for
, for  equal to 5×105, 106, 107, and 108.
equal to 5×105, 106, 107, and 108.
In 1959, Derrick Henry Lehmer extended and simplified Meissel's method. Define, for real  and for natural numbers
and for natural numbers  , and
, and  ,
, 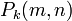 as the number of numbers not greater than m with exactly k prime factors, all greater than
as the number of numbers not greater than m with exactly k prime factors, all greater than 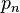 . Furthermore, set
. Furthermore, set  . Then
. Then
where the sum actually has only finitely many nonzero terms. Let  denote an integer such that
denote an integer such that ![{\sqrt[ {3}]{m}}\leq y\leq {\sqrt {m}}](/2014-wikipedia_en_all_02_2014/I/media/d/3/a/a/d3aae4d579779a660acc1578d35c04cf.png) , and set
, and set 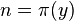 . Then
. Then 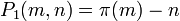 and
and 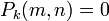 when
when  ≥ 3. Therefore
≥ 3. Therefore
The computation of 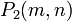 can be obtained this way:
can be obtained this way:
On the other hand, the computation of 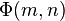 can be done using the following rules:
can be done using the following rules:
Using his method and an IBM 701, Lehmer was able to compute 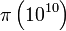 .
.
Further improvements to this method were made by Lagarias, Miller, Odlyzko, Deléglise and Rivat.[11]
The Chinese mathematician Hwang Cheng, in a conference about prime number functions at the University of Bordeaux,[12] used the following identities:
and setting 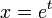 , Laplace-transforming both sides and applying a geometric sum on
, Laplace-transforming both sides and applying a geometric sum on 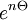 got the expression
got the expression
Other prime-counting functions
Other prime-counting functions are also used because they are more convenient to work with. One is Riemann's prime-counting function, usually denoted as 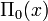 or
or 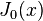 . This has jumps of 1/n for prime powers pn, with it taking a value half-way between the two sides at discontinuities. That added detail is because then it may be defined by an inverse Mellin transform. Formally, we may define
. This has jumps of 1/n for prime powers pn, with it taking a value half-way between the two sides at discontinuities. That added detail is because then it may be defined by an inverse Mellin transform. Formally, we may define 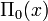 by
by
where p is a prime.
We may also write
where Λ(n) is the von Mangoldt function and
Möbius inversion formula then gives
Knowing the relationship between log of the Riemann zeta function and the von Mangoldt function  , and using the Perron formula we have
, and using the Perron formula we have
The Chebyshev function weights primes or prime powers pn by ln(p):
Riemann's prime-counting function has the ordinary generating function:
Formulas for prime-counting functions
Formulas for prime-counting functions come in two kinds: arithmetic formulas and analytic formulas. Analytic formulas for prime-counting were the first used to prove the prime number theorem. They stem from the work of Riemann and von Mangoldt, and are generally known as explicit formulas.[13]
We have the following expression for ψ:
where
Here ρ are the zeros of the Riemann zeta function in the critical strip, where the real part of ρ is between zero and one. The formula is valid for values of x greater than one, which is the region of interest. The sum over the roots is conditionally convergent, and should be taken in order of increasing absolute value of the imaginary part. Note that the same sum over the trivial roots gives the last subtrahend in the formula.
For 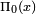 we have a more complicated formula
we have a more complicated formula
Again, the formula is valid for x > 1, while ρ are the nontrivial zeros of the zeta function ordered according to their absolute value, and, again, the latter integral, taken with minus sign, is just the same sum, but over the trivial zeros. The first term li(x) is the usual logarithmic integral function; the expression li(xρ) in the second term should be considered as Ei(ρ ln x), where Ei is the analytic continuation of the exponential integral function from positive reals to the complex plane with branch cut along the negative reals.
Thus, Möbius inversion formula gives us[14]
valid for x > 1, where
is so-called Riemann's R-function.[15] The latter series for it is known as Gram series [16] and converges for all positive x.

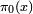 describes the fluctuations of
describes the fluctuations of 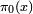 , while the remaining terms give the "smooth" part of prime-counting function,[17] so one can use
, while the remaining terms give the "smooth" part of prime-counting function,[17] so one can use
as the best estimator of 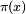 for x > 1.
for x > 1.
The amplitude of the "noisy" part is heuristically about 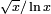 , so the fluctuations of the distribution of primes may be clearly represented with the Δ-function:
, so the fluctuations of the distribution of primes may be clearly represented with the Δ-function:
An extensive table of the values of Δ(x) is available.[7]
Inequalities
Here are some useful inequalities for π(x).
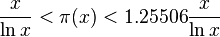 for x ≥ 17.[18]
for x ≥ 17.[18]
The left inequality holds for x ≥ 17 and the right inequality holds for x > 1.
An explanation of the constant 1.25506 is given at (sequence A209883 in OEIS).
Here are some inequalities for the nth prime, pn.[19]
 for n ≥ 6.
for n ≥ 6.
The left inequality holds for n ≥ 1 and the right inequality holds for n ≥ 6.
An approximation for the nth prime number is
The Riemann hypothesis
The Riemann hypothesis is equivalent to a much tighter bound on the error in the estimate for 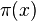 , and hence to a more regular distribution of prime numbers,
, and hence to a more regular distribution of prime numbers,
Specifically,[20]
See also
References
- ↑ Bach, Eric; Shallit, Jeffrey (1996). Algorithmic Number Theory. MIT Press. volume 1 page 234 section 8.8. ISBN 0-262-02405-5.
- ↑ Weisstein, Eric W., "Prime Counting Function", MathWorld.
- ↑ 3.0 3.1 "How many primes are there?". Chris K. Caldwell. Retrieved 2008-12-02.
- ↑ Dickson, Leonard Eugene (2005). History of the Theory of Numbers, Vol. I: Divisibility and Primality. Dover Publications. ISBN 0-486-44232-2.
- ↑ Ireland, Kenneth; Rosen, Michael (1998). A Classical Introduction to Modern Number Theory (Second ed.). Springer. ISBN 0-387-97329-X.
- ↑ "Tables of values of pi(x) and of pi2(x)". Tomás Oliveira e Silva. Retrieved 2008-09-14.
- ↑ 7.0 7.1 "Values of π(x) and Δ(x) for various x's". Andrey V. Kulsha. Retrieved 2008-09-14.
- ↑ "A table of values of pi(x)". Xavier Gourdon, Pascal Sebah, Patrick Demichel. Retrieved 2008-09-14.
- ↑ "Conditional Calculation of pi(1024)". Chris K. Caldwell. Retrieved 2010-08-03.
- ↑ "Computing π(x) Analytically)". Retrieved Jul 25, 2012.
- ↑ "Computing π(x): The Meissel, Lehmer, Lagarias, Miller, Odlyzko method". Marc Deléglise and Jöel Rivat, Mathematics of Computation, vol. 65, number 33, January 1996, pages 235–245. Retrieved 2008-09-14.
- ↑ Hwang H., Cheng (2001). Démarches de la Géométrie et des Nombres de l'Université du Bordeaux. Prime Magic conference
- ↑ Titchmarsh, E.C. (1960). The Theory of Functions, 2nd ed. Oxford University Press.
- ↑ Riesel, Hans; Göhl, Gunnar (1970). "Some calculations related to Riemann's prime number formula". Mathematics of Computation (American Mathematical Society) 24 (112): 969–983. doi:10.2307/2004630. ISSN 0025-5718. JSTOR 2004630. MR 0277489.
- ↑ Weisstein, Eric W., "Riemann Prime Counting Function", MathWorld.
- ↑ Weisstein, Eric W., "Gram Series", MathWorld.
- ↑ "The encoding of the prime distribution by the zeta zeros". Matthew Watkins. Retrieved 2008-09-14.
- ↑ Rosser, J. Barkley; Schoenfeld, Lowell (1962). "Approximate formulas for some functions of prime numbers". Illinois J. Math. 6: 64–94. ISSN 0019-2082. Zbl 0122.05001.
- ↑ Inequalites for the n-th prime number at function.wolfram, retrieved March 22, 2013
- ↑ Schoenfeld, Lowell (1976). "Sharper bounds for the Chebyshev functions θ(x) and ψ(x). II". Mathematics of Computation (American Mathematical Society) 30 (134): 337–360. doi:10.2307/2005976. ISSN 0025-5718. JSTOR 2005976. MR 0457374.
External links
- Chris Caldwell, The Nth Prime Page at The Prime Pages.
- Implementation of Legendre, Meissel, and Lehmer methods in C