Prüfer group

From Wikipedia, the free encyclopedia
The Prüfer 2-group. <gn: gn+12 = gn, g12 = e>

In mathematics, specifically in group theory, the Prüfer p-group or the p-quasicyclic group or p∞-group, Z(p∞), for a prime number p is the unique p-group in which every element has p pth roots. The group is named after Heinz Prüfer. It is a countable abelian group which helps taxonomize infinite abelian groups.

The Prüfer p-group may be represented as a subgroup of the circle group, U(1), as the set of pnth roots of unity as n ranges over all non-negative integers:

{\mathbf {Z}}(p^{\infty })=\{\exp(2\pi im/p^{n})\mid m\in {\mathbf {Z}}^{+},\,n\in {\mathbf {Z}}^{+}\}.\;

Alternatively, the Prüfer p-group may be seen as the Sylow p-subgroup of Q/Z, consisting of those elements whose order is a power of p:

{\mathbf {Z}}(p^{\infty })={\mathbf {Z}}[1/p]/{\mathbf {Z}}

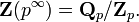
or equivalently {\mathbf {Z}}(p^{\infty })={\mathbf {Q}}_{p}/{\mathbf {Z}}_{p}.

There is a presentation

{\mathbf {Z}}(p^{\infty })=\langle \,x_{1},x_{2},x_{3},\ldots \mid x_{1}^{p}=1,x_{2}^{p}=x_{1},x_{3}^{p}=x_{2},\dots \,\rangle .

The Prüfer p-group is the unique infinite p-group which is locally cyclic (every finite set of elements generates a cyclic group).

The Prüfer p-group is divisible.

In the language of universal algebra, an abelian group is subdirectly irreducible if and only if it is isomorphic to a finite cyclic p-group or isomorphic to a Prüfer group.

In the theory of locally compact topological groups the Prüfer p-group (endowed with the discrete topology) is the Pontryagin dual of the compact group of p-adic integers, and the group of p-adic integers is the Pontryagin dual of the Prüfer p-group.[1]

The Prüfer p-groups for all primes p are the only infinite groups whose subgroups are totally ordered by inclusion. As there is no maximal subgroup of a Prüfer p-group, it is its own Frattini subgroup.

0\subset {\mathbf {Z}}/p\subset {\mathbf {Z}}/p^{2}\subset {\mathbf {Z}}/p^{3}\subset \cdots \subset {\mathbf {Z}}(p^{\infty })

This sequence of inclusions expresses the Prüfer p-group as the direct limit of its finite subgroups.

As a {\mathbf {Z}}-module, the Prüfer p-group is Artinian, but not Noetherian, and likewise as a group, it is Artinian but not Noetherian.[2][3] It can thus be used as a counterexample against the idea that every Artinian module is Noetherian (whereas every Artinian ring is Noetherian).

See also

  • p-adic integers, which can be defined as the inverse limit of the finite subgroups of the Prüfer p-group.
  • Dyadic rational, rational numbers of the form a/2b. The Prüfer 2-group can be viewed as the dyadic rationals modulo 1.

Notes

  1. ↑ D. L. Armacost and W. L. Armacost, "On p-thetic groups", Pacific J. Math., 41, no. 2 (1972), 295–301
  2. ↑ Subgroups of an abelian group are abelian, and coincide with submodules as a {\mathbf {Z}}-module.
  3. ↑ See also Jacobson (2009), p. 102, ex. 2.

References

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.