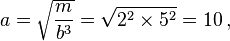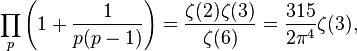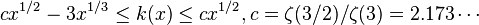Powerful number

From Wikipedia, the free encyclopedia

A powerful number is a positive integer m such that for every prime number p dividing m, p² also divides m. Equivalently, a powerful number is the product of a square and a cube, that is, a number m of the form m = a²b³, where a and b are positive integers. Powerful numbers are also known as squareful, square-full, or 2-full. Paul Erdős and George Szekeres studied such numbers and Solomon W. Golomb named such numbers powerful.

The following is a list of all powerful numbers between 1 and 1000:

1, 4, 8, 9, 16, 25, 27, 32, 36, 49, 64, 72, 81, 100, 108, 121, 125, 128, 144, 169, 196, 200, 216, 225, 243, 256, 288, 289, 324, 343, 361, 392, 400, 432, 441, 484, 500, 512, 529, 576, 625, 648, 675, 676, 729, 784, 800, 841, 864, 900, 961, 968, 972, 1000 (sequence A001694 in OEIS).

Equivalence of the two definitions

If m = a²b³, then every prime in the prime factorization of a appears in the prime factorization of m with an exponent of at least two, and every prime in the prime factorization of b appears in the prime factorization of m with an exponent of at least three; therefore, m is powerful.

In the other direction, suppose that m is powerful, with prime factorization

$m=\prod p_{i}^{{\alpha _{i}}},$

where each α_i ≥ 2. Define γ_i to be three if α_i is odd, and zero otherwise, and define β_i = α_i - γ_i. Then, all values β_i are nonnegative even integers, and all values γ_i are either zero or three, so

$m=(\prod p_{i}^{{\beta _{i}}})(\prod p_{i}^{{\gamma _{i}}})=(\prod p_{i}^{{\beta _{i}/2}})^{2}(\prod p_{i}^{{\gamma _{i}/3}})^{3}$

supplies the desired representation of m as a product of a square and a cube.

Informally, given the prime factorization of m, take b to be the product of the prime factors of m that have an odd exponent (if there are none, then take b to be 1). Because m is powerful, each prime factor with an odd exponent has an exponent that is at least 3, so m/b³ is an integer. In addition, each prime factor of m/b³ has an even exponent, so m/b³ is a perfect square, so call this a²; then m = a²b³. For example:

$m=21600=2^{5}\times 3^{3}\times 5^{2}\,,$

$b=2\times 3=6\,,$

$a={\sqrt {{\frac {m}{b^{3}}}}}={\sqrt {2^{2}\times 5^{2}}}=10\,,$

$m=a^{2}b^{3}=10^{2}\times 6^{3}\,.$

The representation m = a²b³ calculated in this way has the property that b is squarefree, and is uniquely defined by this property.

Mathematical properties

The Dirichlet series generating function for powerful numbers is

${\frac {\zeta (2s)\zeta (3s)}{\zeta (6s)}}\$

and so the sum of reciprocals of powerful numbers converges to

$\prod _{p}\left(1+{\frac {1}{p(p-1)}}\right)={\frac {\zeta (2)\zeta (3)}{\zeta (6)}}={\frac {315}{2\pi ^{4}}}\zeta (3),$

where p runs over all primes, ζ(s) denotes the Riemann zeta function, and ζ(3) is Apéry's constant (Golomb, 1970).

Let k(x) denote the number of powerful numbers in the interval [1,x]. Then k(x) is proportional to the square root of x. More precisely,

$cx^{{1/2}}-3x^{{1/3}}\leq k(x)\leq cx^{{1/2}},c=\zeta (3/2)/\zeta (3)=2.173\cdots$

(Golomb, 1970).

The two smallest consecutive powerful numbers are 8 and 9. Since Pell's equation x² − 8y² = 1 has infinitely many integral solutions, there are infinitely many pairs of consecutive powerful numbers (Golomb, 1970); more generally, one can find consecutive powerful numbers by solving a similar Pell equation x² − ny² = ±1 for any perfect cube n. However, one of the two powerful numbers in a pair formed in this way must be a square. According to Guy, Erdős has asked whether there are infinitely many pairs of consecutive powerful numbers such as (23³, 2³3²13²) in which neither number in the pair is a square. Jaroslaw Wroblewski showed that there are indeed infinitely many such pairs by showing that 3³c²+1=7³d² has infinitely many solutions. It is a conjecture of Erdős, Mollin, and Walsh that there are no three consecutive powerful numbers.

Sums and differences of powerful numbers

Any odd number is a difference of two consecutive squares: (k + 1)² = k² + 2k +1², so (k + 1)² - k² = 2k + 1. Similarly, any multiple of four is a difference of the squares of two numbers that differ by two: (k + 2)² - k² = 4k + 4. However, a singly even number, that is, a number divisible by two but not by four, cannot be expressed as a difference of squares. This motivates the question of determining which singly even numbers can be expressed as differences of powerful numbers. Golomb exhibited some representations of this type:

2 = 3³ − 5²

10 = 13³ − 3⁷

18 = 19² − 7³ = 3²(3³ − 5²).

It had been conjectured that 6 cannot be so represented, and Golomb conjectured that there are infinitely many integers which cannot be represented as a difference between two powerful numbers. However, Narkiewicz showed that 6 can be so represented in infinitely many ways such as

6 = 5⁴7³ − 463²,

and McDaniel showed that every integer has infinitely many such representations (McDaniel, 1982).

Erdős conjectured that every sufficiently large integer is a sum of at most three powerful numbers; this was proved by Roger Heath-Brown (1987).

Generalization

More generally, we can consider the integers all of whose prime factors have exponents at least k. Such an integer is called a k-powerful number, k-ful number, or k-full number.

(2^k+1 − 1)^k, 2^k(2^k+1 − 1)^k, (2^k+1 − 1)^k+1

are k-powerful numbers in an arithmetic progression. Moreover, if a₁, a₂, ..., a_s are k-powerful in an arithmetic progression with common difference d, then

a₁(a_s + d)^k,

a₂(a_s + d)^k, ..., a_s(a_s + d)^k, (a_s + d)^k+1

are s + 1 k-powerful numbers in an arithmetic progression.

We have an identity involving k-powerful numbers:

a^k(a^l + ... + 1)^k + a^{k + 1}(a^l + ... + 1)^k + ... + a^{k + l}(a^l + ... + 1)^k = a^k(a^l + ... +1)^k+1.

This gives infinitely many l+1-tuples of k-powerful numbers whose sum is also k-powerful. Nitaj shows there are infinitely many solutions of x+y=z in relatively prime 3-powerful numbers(Nitaj, 1995). Cohn constructs an infinite family of solutions of x+y=z in relatively prime non-cube 3-powerful numbers as follows: the triplet

X = 9712247684771506604963490444281, Y = 32295800804958334401937923416351, Z = 27474621855216870941749052236511

is a solution of the equation 32X³ + 49Y³ = 81Z³. We can construct another solution by setting X′ = X(49Y³ + 81Z³), Y′ = −Y(32X³ + 81Z³), Z′ = Z(32X³ − 49Y³) and omitting the common divisor.

References

Cohn, J. H. E. (1998). "A conjecture of Erdős on 3-powerful numbers". Math. Comp. 67 (221): 439–440. doi:10.1090/S0025-5718-98-00881-3.
Erdős, Paul and Szekeres, George (1934). "Über die Anzahl der Abelschen Gruppen gegebener Ordnung und über ein verwandtes zahlentheoretisches Problem". Acta Litt. Sci. Szeged 7: 95–102.
Golomb, Solomon W. (1970). "Powerful numbers". American Mathematical Monthly 77 (8): 848–852. doi:10.2307/2317020. JSTOR 2317020.
Guy, Richard K. (2004). Unsolved Problems in Number Theory, 3rd edition. Springer-Verlag. Section B16. ISBN 0-387-20860-7.
Heath-Brown, Roger (1988). "Ternary quadratic forms and sums of three square-full numbers". Séminaire de Théorie des Nombres, Paris, 1986-7. Boston: Birkhäuser. pp. 137–163.
Heath-Brown, Roger (1990). "Sums of three square-full numbers". Number Theory, I (Budapest, 1987). Colloq. Math. Soc. János Bolyai, no. 51. pp. 163–171.
Ivić, Aleksandar (1985). The Riemann zeta-function. The theory of the Riemann zeta-function with applications. A Wiley-Interscience Publication. New York etc.: John Wiley & Sons. pp. 33–34,407–413. ISBN 0-471-80634-X. Zbl 0556.10026.
McDaniel, Wayne L. (1982). "Representations of every integer as the difference of powerful numbers". Fibonacci Quarterly 20: 85–87.
Nitaj, Abderrahmane (1995). "On a conjecture of Erdős on 3-powerful numbers". Bull. London Math. Soc. 27 (4): 317–318. doi:10.1112/blms/27.4.317.

External links

Weisstein, Eric W., "Powerful number", MathWorld.
The abc conjecture
"Sloane's A060355 : Numbers n such that n and n+1 are a pair of consecutive powerful numbers", The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.

v t e Divisibility-based sets of integers

Overview	Integer factorization Divisor Unitary divisor Divisor function Prime factor Fundamental theorem of arithmetic Arithmetic number

Factorization forms	Prime number Composite number Semiprime number Pronic number Sphenic number Square-free number Powerful number Perfect power Achilles number Smooth number Regular number Rough number Unusual number

Constrained divisor sums	Perfect number Almost perfect number Quasiperfect number Multiply perfect number Hemiperfect number Hyperperfect number Superperfect number Unitary perfect number Semiperfect number Practical number

With many divisors	Abundant number Primitive abundant number Highly abundant number Superabundant number Colossally abundant number Highly composite number Superior highly composite number Weird number

Aliquot sequence-related	Untouchable number Amicable number Sociable number Betrothed number

Other sets	Deficient number Friendly number Solitary number Sublime number Harmonic divisor number Frugal number Equidigital number Extravagant number

Classes of natural numbers

Powers and
related numbers

Of the form
a × 2^b ± 1

other polynomial
numbers

Recursively defined
numbers

Possessing a
specific set
of other numbers

Expressible via
specific sums

Generated
via a sieve

Lucky numbers

Code related

Meertens numbers

Figurate numbers

2-dimensional

centered	Centered triangular numbers Centered square numbers Centered pentagonal numbers Centered hexagonal numbers Centered heptagonal numbers Centered octagonal numbers Centered nonagonal numbers Centered decagonal numbers Star numbers

non-centered	Triangular numbers Pentagonal numbers Hexagonal numbers Heptagonal numbers Octagonal numbers Nonagonal numbers Decagonal numbers Dodecagonal numbers

3-dimensional

centered	Centered tetrahedral numbers Centered cube numbers Centered octahedral numbers Centered dodecahedral numbers Centered icosahedral numbers

non-centered	Tetrahedral numbers Octahedral numbers Dodecahedral numbers Icosahedral numbers Stella octangula numbers

pyramidal	Square pyramidal numbers Pentagonal pyramidal numbers Hexagonal pyramidal numbers Heptagonal pyramidal numbers

4-dimensional

centered	Centered pentachoric numbers Squared triangular numbers

non-centered	Pentatope numbers

Pseudoprimes

Combinatorial
numbers

Arithmetic functions

By properties of σ(n)	Abundant numbers Almost perfect numbers Arithmetic numbers Colossally abundant numbers Descartes numbers Hemiperfect numbers Highly abundant numbers Hyperperfect numbers Multiply perfect numbers Perfect numbers Primitive abundant numbers Quasiperfect numbers Refactorable numbers Sublime numbers Superabundant numbers Superior highly composite numbers Superperfect numbers

By properties of Ω(n)	Almost primes Semiprimes

By properties of φ(n)	Highly cototient numbers Highly totient numbers Noncototients Nontotients Perfect totient numbers Sparsely totient numbers

By properties of s(n)	Amicable numbers Betrothed numbers Deficient numbers Semiperfect numbers

Dividing a quotient

Wieferich numbers
Wilson numbers

Other prime factor
or divisor related
numbers

Recreational
mathematics

Base-dependent
numbers

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.