Power center (geometry)
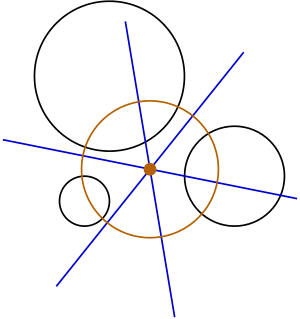
In geometry, the power center of three circles, also called the radical center, is the intersection point of the three radical axes of the pairs of circles. If the radical center lies outside of all three circles, then it is the center of the unique circle (the radical circle) that intersects the three given circles orthogonally; the construction of this orthogonal circle corresponds to Monge's problem. This is a special case of the three conics theorem.
The three radical axes meet in a single point, the radical center, for the following reason. The radical axis of a pair of circles is defined as the set of points that have equal power h with respect to both circles. For example, for every point P on the radical axis of circles 1 and 2, the powers to each circle are equal, h1 = h2. Similarly, for every point on the radical axis of circles 2 and 3, the powers must be equal, h2 = h3. Therefore, at the intersection point of these two lines, all three powers must be equal, h1 = h2 = h3. Since this implies that h1 = h3, this point must also lie on the radical axis of circles 1 and 3. Hence, all three radical axes pass through the same point, the radical center.
The radical center has several applications in geometry. It has an important role in a solution to Apollonius' problem published by Joseph Diaz Gergonne in 1814. Several types of radical circles have been defined as well, such as the radical circle of the Lucas circles.
See also
Further reading
- Ogilvy CS (1990). Excursions in Geometry. Dover. p. 23. ISBN 0-486-26530-7
- Coxeter HSM, Greitzer SL (1967). Geometry Revisited. Washington: MAA. pp. 35, 38. ISBN 978-0-88385-619-2.
- Johnson RA (1960). Advanced Euclidean Geometry: An elementary treatise on the geometry of the triangle and the circle (reprint of 1929 edition by Houghton Miflin ed.). New York: Dover Publications. pp. 32–34. ISBN 978-0-486-46237-0.
- Wells D (1991). The Penguin Dictionary of Curious and Interesting Geometry. New York: Penguin Books. p. 35. ISBN 0-14-011813-6.
- Dörrie H (1965). "Monge's Problem". 100 Great Problems of Elementary Mathematics: Their History and Solutions. New York: Dover. pp. 151–154 (§31).
- Lachlan R (1893). An elementary treatise on modern pure geometry. London: Macmillan. p. 185. ASIN B0008CQ720.
External links
| Wikimedia Commons has media related to Radical centers and axes. |
- Weisstein, Eric W., "Radical center", MathWorld.
- Weisstein, Eric W., "Radical circle", MathWorld.
- Weisstein, Eric W., "Monge's problem", MathWorld.
- Radical Center at Cut-the-Knot
- Radical Axis and Center at Cut-the-Knot