Potential vorticity

From Wikipedia, the free encyclopedia

Potential vorticity (PV) is a quantity which is proportional to the dot product of vorticity and stratification that, following a parcel of air or water, can only be changed by diabatic or frictional processes. It is a useful concept for understanding the generation of vorticity in cyclogenesis (the birth and development of a cyclone), especially along the polar front, and in analyzing flow in the ocean.

In meteorology, the potential vorticity unit (PVU) is defined as 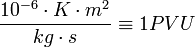{10^{{-6}}\cdot K\cdot m^{2} \over kg\cdot s}\equiv 1PVU.

It is also useful in tracing intrusions of stratospheric air deep into the troposphere in the vicinity of jet streaks, a concentrated region within a jet stream where the wind speeds are the strongest. It acts as a flow tracer in the ocean as well. It can also be used to explain how a range of mountains like the Andes can make the upper westerly winds swerve towards the equator and back.

Baroclinic instability requires the presence of a potential vorticity gradient along which waves amplify during cyclogenesis.

PV conservation

Convergence and divergence of an air parcel

Carl-Gustaf Rossby first introduced potential vorticity in his 1936 paper "Dynamics of steady ocean currents in the light of experimental fluid mechanics". This work was based on an analysis of a shallow water model of the Gulf Stream. The concept was developed further, within a few years of Rossby's seminal paper, by Hans Ertel. Mathematically, Ertel's form of potential vorticity is given by the equation:

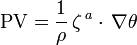
{{\rm {PV}}}={\frac {1}{\rho }}\,\zeta \,^{a}\cdot \,\nabla \theta

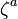where \rho is the fluid density, \zeta ^{a} is the absolute vorticity and \nabla \theta is the gradient of the potential temperature. It can be shown through a combination of the first law of thermodynamics and momentum conservation that potential vorticity can only be changed by diabatic heating (such as latent heat released from condensation) or frictional processes. This conservation is the atmospheric equivalent to inertia. A spinning ice skater with her arms spread out laterally can accelerate her rate of spin by contracting her arms. Similarly, when a vortex of air is broad, it is in turn, slow. When the air converges, to maintain potential vorticity, the air speed increases, resulting in a stretched ring vortex. Divergence causes the vortex to spread, slowing down the rate of spin.

See also

Further reading

  • Hoskins, B.J., McIntyre, M.E. and Robertson, A.W. "On the use and significance of isentropic potential vorticity maps". Quarterly Journal of the Royal Meteorological Society, volume 111 (1985): 877-946.
  • Rossby, C-G. "Dynamics of steady ocean currents in the light of experimental fluid mechanics". Papers in Physical Oceanography and Meteorology, volume 5 (1936): 2-43.
  • Roulstone, Ian; Norbury, John (2013). Invisible in the Storm: the role of mathematics in understanding weather. Princeton: Princeton University Press. ISBN 978-0-691-15272-1. 
  • Thorpe, A.J., Volkert, H. and Ziemiański, M.J. "The Bjerknes' circulation theorem: a historical perspective." Bulletin of the American Meteorological Society, volume 84 (2003): 471-480.

External links

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.