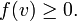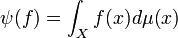Positive linear functional

From Wikipedia, the free encyclopedia

In mathematics, especially in functional analysis, a positive linear functional on an ordered vector space (V, ≤) is a linear functional f on V so that for all positive elements v of V, that is v≥0, it holds that

$f(v)\geq 0.$

In other words, a positive linear functional is guaranteed to take nonnegative values for positive elements. The significance of positive linear functionals lies in results such as Riesz–Markov–Kakutani representation theorem.

Examples

Consider, as an example of V, the C*-algebra of complex square matrices with the positive elements being the positive-definite matrices. The trace function defined on this C*-algebra is a positive functional, as the eigenvalues of any positive-definite matrix are positive, and so its trace is positive.

Consider the Riesz space C_c(X) of all continuous complex-valued functions of compact support on a locally compact Hausdorff space X. Consider a Borel regular measure μ on X, and a functional ψ defined by

$\psi (f)=\int _{X}f(x)d\mu (x)\quad$

for all f in C_c(X). Then, this functional is positive (the integral of any positive function is a positive number). Moreover, any positive functional on this space has this form, as follows from the Riesz–Markov–Kakutani representation theorem.

v t e Functional analysis

Local Notions on Sets	Absolutely convex Absorbing Balanced Bounded Cones (Linear, Convex cone) Convex Radial Star-shaped Symmetric

Types of TVSs	Banach Barrelled Bornological Brauner F-space Finite-dimensional Fréchet (Tame) Hilbert LF Locally convex Mackey Montel Nuclear Normed (Norm) Reflexive Riesz Smith Stereotype Topological tensor product (of Hilbert spaces) Webbed

Spaces of Maps	Dual space Dual topology Operator topologies Strong Topology (Polar, Operator) Topology of uniform convergence Weak topology (operator) Ultrastrong topology Ultraweak topology

Types of Linear operators	Adjoint Bilinear (form) Bounded (Unbounded) Closed Continuous (Discontinuous) Compact Fredholm Hilbert–Schmidt Functionals (Positive) Normal Nuclear Self-adjoint Strictly singular Trace class Transpose Unitary

Operations on Sets	Algebraic interior (core) Interior Minkowski addition Polar

Banach Algebras	C-algebras Spectrum (of a C-algebra, Spectral radius) Spectral theory

Important Theorems	Banach–Alaoglu Banach–Saks Banach–Mazur Bessel's inequality Cauchy–Schwarz inequality Closed range Closed graph Eberlein–Šmulian Freudenthal spectral Gelfand–Mazur Goldstine Hahn–Banach (Hyperplane separation) Kakutani fixed-point Lomonosov's Invariant Subspace Mackey–Arens Mazur's lemma M. Riesz extension Open mapping Parseval's identity Schauder fixed-point

Analysis	Bochner space Derivatives (Fréchet derivative, Gâteaux derivative, Functional, Holomorphy) Differentiation in Fréchet spaces Integrals (Bochner, Dunford, Gelfand–Pettis, Regulated, Weak) Functional calculus Inverse function theorem (Nash–Moser theorem) Vector measure

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.

Positive linear functional

Examples

See also