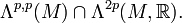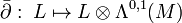Positive form

From Wikipedia, the free encyclopedia

In complex geometry, the term positive form refers to several classes of real differential forms of Hodge type (p, p).

(1,1)-forms

Real (p,p)-forms on a complex manifold M are forms which are of type (p,p) and real, that is, lie in the intersection

$\Lambda ^{{p,p}}(M)\cap \Lambda ^{{2p}}(M,{{\mathbb R}}).$

A real (1,1)-form 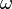$\omega$ is called positive if any of the following equivalent conditions hold

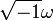${\sqrt {-1}}\omega$ is an imaginary part of a positive (not necessarily positive definite) Hermitian form.
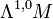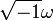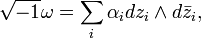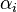For some basis $dz_{1},...dz_{n}$ in the space $\Lambda ^{{1,0}}M$ of (1,0)-forms, ${\sqrt {-1}}\omega$ can be written diagonally, as ${\sqrt {-1}}\omega =\sum _{i}\alpha _{i}dz_{i}\wedge d{\bar z}_{i},$ with $\alpha _{i}$ real and non-negative.
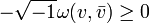
For any (1,0)-tangent vector $v\in T^{{1,0}}M$ , $-{\sqrt {-1}}\omega (v,{\bar v})\geq 0$
For any real tangent vector 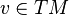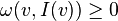$v\in TM$ , $\omega (v,I(v))\geq 0$ , where 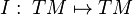$I:\;TM\mapsto TM$ is the complex structure operator.

Positive line bundles

In algebraic geometry, positive (1,1)-forms arise as curvature forms of ample line bundles (also known as positive line bundles). Let L be a holomorphic Hermitian line bundle on a complex manifold,

${\bar \partial }:\;L\mapsto L\otimes \Lambda ^{{0,1}}(M)$

its complex structure operator. Then L is equipped with a unique connection preserving the Hermitian structure and satisfying

$\nabla ^{{0,1}}={\bar \partial }$ .

This connection is called the Chern connection.

The curvature 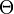$\Theta$ of a Chern connection is always a purely imaginary (1,1)-form. A line bundle L is called positive if

${\sqrt {-1}}\Theta$

is a positive definite (1,1)-form. The Kodaira embedding theorem claims that a positive line bundle is ample, and conversely, any ample line bundle admits a Hermitian metric with 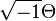${\sqrt {-1}}\Theta$ positive.

Positivity for (p, p)-forms

Positive (1,1)-forms on M form a convex cone. When M is a compact complex surface, $dim_{{{\mathbb C}}}M=2$ , this cone is self-dual, with respect to the Poincaré pairing

$\eta ,\zeta \mapsto \int _{M}\eta \wedge \zeta$

For (p, p)-forms, where 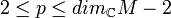$2\leq p\leq dim_{{{\mathbb C}}}M-2$ , there are two different notions of positivity. A form is called strongly positive if it is a linear combination of products of positive forms, with positive real coefficients. 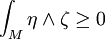A real (p, p)-form $\eta$ on an n-dimensional complex manifold M is called weakly positive if for all strongly positive (n-p, n-p)-forms ζ with compact support, we have $\int _{M}\eta \wedge \zeta \geq 0$ .

Weakly positive and strongly positive forms form convex cones. On compact manifolds these cones are dual with respect to the Poincaré pairing.

References

Phillip Griffiths and Joseph Harris (1978), Principles of Algebraic Geometry, Wiley. ISBN 0-471-32792-1

J.-P. Demailly, L² vanishing theorems for positive line bundles and adjunction theory, Lecture Notes of a CIME course on "Transcendental Methods of Algebraic Geometry" (Cetraro, Italy, July 1994).

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.