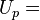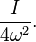Ponderomotive energy

From Wikipedia, the free encyclopedia

In strong field laser physics, the term Ponderomotive Energy^[1] refers to the cycle averaged quiver energy of a free electron in an E-field.

Equation

The Ponderomotive Energy equation is given by,

$U_{p}=$ $e^{2}$ $E_{a}^{2}$ $/4m$ $\omega _{0}^{2}$

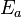Where $e$ is the electron charge, $E_{a}$ is the linearly polarised electric field amplitude, 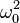$\omega _{0}^{2}$ is the laser carrier frequency and $m$ is the electron mass.

Description

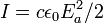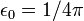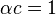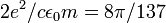In terms of the laser intensity $I$ , using $I=c\epsilon _{0}E_{a}^{2}/2$ , it reads less simply $U_{p}=e^{2}I/2c\epsilon _{0}m\omega _{0}^{2}=2e^{2}/c\epsilon _{0}m\times I/4\omega _{0}^{2}$ . Now, atomic units provide $e=m=1$ , $\epsilon _{0}=1/4\pi$ , $\alpha c=1$ where $\alpha \approx 1/137$ . Thus, $2e^{2}/c\epsilon _{0}m=8\pi /137$ .

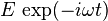The formula for the ponderomotive energy can be easily derived. A free electron of charge $e$ interacts with an electric field $E\,\exp(-i\omega t)$ . The force on the electron is

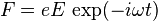$F=eE\,\exp(-i\omega t)$ .

The acceleration of the electron is

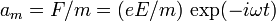$a_{{m}}=F/m=(eE/m)\,\exp(-i\omega t)$ .

Because the electron executes harmonic motion, the electron's position is

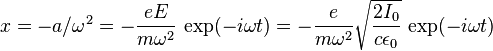$x=-a/\omega ^{2}=-{\frac {eE}{m\omega ^{2}}}\,\exp(-i\omega t)=-{\frac {e}{m\omega ^{2}}}{\sqrt {{\frac {2I_{0}}{c\epsilon _{0}}}}}\,\exp(-i\omega t)$ .

For a particle experiencing harmonic motion, the time-averaged energy is

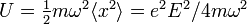$U=\textstyle {{\frac {1}{2}}}m\omega ^{2}\langle x^{2}\rangle =e^{2}E^{2}/4m\omega ^{2}$ .

In laser physics, this is called the ponderomotive energy $U_{p}$ .

Atomic units

References and notes

↑ Highly Excited Atoms. By J. P. Connerade. p339
↑ CODATA Value: atomic unit of electric field

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.

Ponderomotive energy

Equation

Description

Atomic units

See also

References and notes