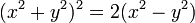Polynomial lemniscate
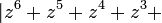
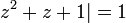
In mathematics, a polynomial lemniscate or polynomial level curve is a plane algebraic curve of degree 2n, constructed from a polynomial p with complex coefficients of degree n.
For any such polynomial p and positive real number c, we may define a set of complex numbers by 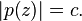 This set of numbers may be equated to points in the real Cartesian plane, leading to an algebraic curve ƒ(x, y) = c2 of degree 2n, which results from expanding out
This set of numbers may be equated to points in the real Cartesian plane, leading to an algebraic curve ƒ(x, y) = c2 of degree 2n, which results from expanding out 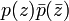 in terms of z = x + iy.
in terms of z = x + iy.
When p is a polynomial of degree 1 then the resulting curve is simply a circle whose center is the zero of p. When p is a polynomial of degree 2 then the curve is a Cassini oval.
Erdős lemniscate

A conjecture of Erdős which has attracted considerable interest concerns the maximum length of a polynomial lemniscate ƒ(x, y) = 1 of degree 2n when p is monic, which Erdős conjectured was attained when p(z) = zn − 1. This is still not proved but Fryntov and Nazarov proved that p gives a local maximum.[1] In the case when n = 2, the Erdős lemniscate is the Lemniscate of Bernoulli
and it has been proven that this is indeed the maximal length in degree four. The Erdős lemniscate has three ordinary n-fold points, one of which is at the origin, and a genus of (n − 1)(n − 2)/2. By inverting the Erdős lemniscate in the unit circle, one obtains a nonsingular curve of degree n.
Generic polynomial lemniscate
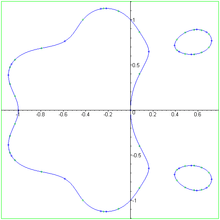
In general, a polynomial lemniscate will not touch at the origin, and will have only two ordinary n-fold singularities, and hence a genus of (n − 1)2. As a real curve, it can have a number of disconnected components. Hence, it will not look like a lemniscate, making the name something of a misnomer.
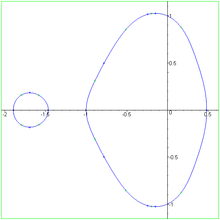
An interesting example of such polynomial lemniscates are the Mandelbrot curves. If we set p0 = z, and pn = pn−12 + z, then the corresponding polynomial lemniscates Mn defined by |pn(z)| = 1 converge to the boundary of the Mandelbrot set. The Mandelbrot curves are of degree 2n+1.[2]
Notes
- ↑ Fryntov, A; Nazarov, F (2008). "New estimates for the length of the Erdos-Herzog-Piranian lemniscate". Linear and Complex Analysis 226: 49–60.
- ↑ Ivancevic, Vladimir G.; Ivancevic, Tijana T. (2007), High-Dimensional Chaotic and Attractor Systems: A Comprehensive Introduction, Springer, p. 492, ISBN 9781402054563.
References
- Alexandre Eremenko and Walter Hayman, On the length of lemniscates, Michigan Math. J., (1999), 46, no. 2, 409–415
- O. S. Kusnetzova and V. G. Tkachev, Length functions of lemniscates, Manuscripta Math., (2003), 112, 519–538
- "Cassinian curve" at Encyclopédie des Formes Mathématiques Remarquables