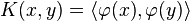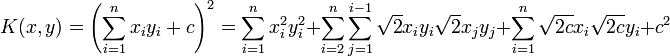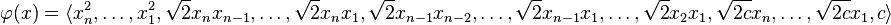Polynomial kernel

From Wikipedia, the free encyclopedia

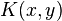Illustration of the mapping $\varphi$ . On the left a set of samples in the input space, on the right the same samples in the feature space where the polynomial kernel $K(x,y)$ (for some values of the parameters $c$ and $d$ is the inner product. The hyperplane learned in feature space by an SVM is an ellipse in the input space.

In machine learning, the polynomial kernel is a kernel function commonly used with support vector machines (SVMs) and other kernelized models, that represents the similarity of vectors (training samples) in a feature space over polynomials of the original variables, allowing learning of non-linear models.

Intuitively, the polynomial kernel looks not only at the given features of input samples to determine their similarity, but also combinations of these.

Definition

For degree-d polynomials, the polynomial kernel is defined as^[1]

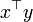$K(x,y)=(x^{\top }y+c)^{d}$

where $x$ and $y$ are vectors in the input space, i.e. vectors of features computed from training or test samples, $c\geq 0$ is a constant trading off the influence of higher-order versus lower-order terms in the polynomial. When $c=0$ , the kernel is called homogeneous.^[2] (A further generalized polykernel divides $x^{\top }y$ by a user-specified scalar parameter $a$ .^[3])

As a kernel, $K$ corresponds an inner product in a feature space based on some mapping $\varphi$ :

$K(x,y)=\langle \varphi (x),\varphi (y)\rangle$

The nature of $\varphi$ can be glanced from an example. Let $d=2$ , so we get the special case of the quadratic kernel. Then

$K(x,y)=\left(\sum _{{i=1}}^{n}x_{i}y_{i}+c\right)^{2}=\sum _{{i=1}}^{n}x_{i}^{2}y_{i}^{2}+\sum _{{i=2}}^{n}\sum _{{j=1}}^{{i-1}}{\sqrt {2}}x_{i}y_{i}{\sqrt {2}}x_{j}y_{j}+\sum _{{i=1}}^{n}{\sqrt {2c}}x_{i}{\sqrt {2c}}y_{i}+c^{2}$

From this it follows that the feature map is given by:

$\varphi (x)=\langle x_{n}^{2},\ldots ,x_{1}^{2},{\sqrt {2}}x_{n}x_{{n-1}},\ldots ,{\sqrt {2}}x_{n}x_{1},{\sqrt {2}}x_{{n-1}}x_{{n-2}},\ldots ,{\sqrt {2}}x_{{n-1}}x_{{1}},\ldots ,{\sqrt {2}}x_{{2}}x_{{1}},{\sqrt {2c}}x_{n},\ldots ,{\sqrt {2c}}x_{1},c\rangle$

When the input features are binary-valued (booleans), $c=1$ and the ${\sqrt {2}}$ terms are ignored, the mapped features correspond to conjunctions of input features.^[4]

Practical use

Although the RBF kernel is more popular in SVM classification than the polynomial kernel, the latter is quite popular in natural language processing (NLP).^[4]^[5] The most common degree is d=2, since larger degrees tend to overfit on NLP problems.

Various ways of computing the polynomial kernel (both exact and approximate) have been devised as alternatives to the usual non-linear SVM training algorithms, including:

full expansion of the kernel prior to training/testing with a linear SVM,^[5] i.e. full computation of the mapping $\varphi$
basket mining (using a variant of the apriori algorithm) for the most commonly occurring feature conjunctions in a training set to produce an approximate expansion^[6]
inverted indexing of support vectors^[6]^[4]

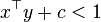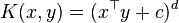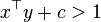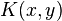One problem with the polynomial kernel is that may it suffer from numerical instability: when $x^{\top }y+c<1$ , $K(x,y)=(x^{\top }y+c)^{d}$ tends to zero as $d$ is increased, whereas when $x^{\top }y+c>1$ , $K(x,y)$ tends to infinity.^[3]

References

↑ http://www.cs.tufts.edu/~roni/Teaching/CLT/LN/lecture18.pdf
↑ Shashua, Amnon (2009). "Introduction to Machine Learning: Class Notes 67577". arXiv:0904.3664v1 [cs.LG].
↑ 3.0 3.1 Chih-Jen Lin (2012). Machine learning software: design and practical use. Talk at Machine Learning Summer School, Kyoto.
↑ 4.0 4.1 4.2 Yoav Goldberg and Michael Elhadad (2008). splitSVM: Fast, Space-Efficient, non-Heuristic, Polynomial Kernel Computation for NLP Applications. Proc. ACL-08: HLT.
↑ 5.0 5.1 Yin-Wen Chang, Cho-Jui Hsieh, Kai-Wei Chang, Michael Ringgaard and Chih-Jen Lin (2010). Training and testing low-degree polynomial data mappings via linear SVM. J. Machine Learning Research 11:1471–1490.
↑ 6.0 6.1 T. Kudo and Y. Matsumoto (2003). Fast methods for kernel-based text analysis. Proc. ACL 2003.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.