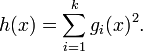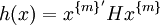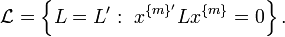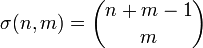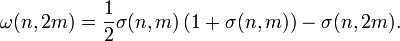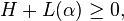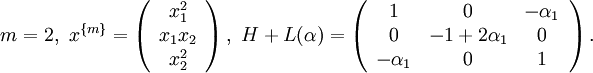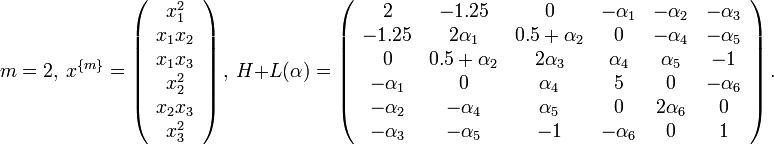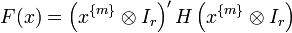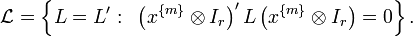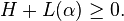Polynomial SOS

From Wikipedia, the free encyclopedia

This article is about representing polynomial as sum of squares of polynomials. For representing polynomial as a sum of squares of rational functions, see Hilbert's seventeenth problem. For the sum of squares of consecutive integers, see square pyramidal number. For representing an integer as a sum of squares of integers, see Lagrange's four-square theorem.

In mathematics, a form (i.e. a homogeneous polynomial) h(x) of degree 2m in the real n-dimensional vector x is sum of squares of forms (SOS) if and only if there exist forms 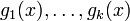$g_{1}(x),\ldots ,g_{k}(x)$ of degree m such that

$h(x)=\sum _{{i=1}}^{k}g_{i}(x)^{2}.$

Explicit sufficient conditions for a form to be SOS have been found.^[1] However every real nonnegative form can be approximated as closely as desired (in the 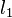$l_{1}$ -norm of its coefficient vector) by a sequence of forms $\{f_{\epsilon }\}$ that are SOS.^[2]

Square matricial representation (SMR)

To establish whether a form h(x) is SOS amounts to solving a convex optimization problem. Indeed, any h(x) can be written as

$h(x)=x^{{\{m\}'}}\left(H+L(\alpha )\right)x^{{\{m\}}}$

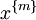where $x^{{\{m\}}}$ is a vector containing a base for the forms of degree m in x (such as all monomials of degree m in x), the prime ′ denotes the transpose, H is any symmetric matrix satisfying

$h(x)=x^{{\left\{m\right\}'}}Hx^{{\{m\}}}$

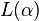and $L(\alpha )$ is a linear parameterization of the linear space

${\mathcal {L}}=\left\{L=L':~x^{{\{m\}'}}Lx^{{\{m\}}}=0\right\}.$

The dimension of the vector 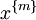$x^{{\{m\}}}$ is given by

$\sigma (n,m)={\binom {n+m-1}{m}}$

whereas the dimension of the vector $\alpha$ is given by

$\omega (n,2m)={\frac {1}{2}}\sigma (n,m)\left(1+\sigma (n,m)\right)-\sigma (n,2m).$

Then, h(x) is SOS if and only if there exists a vector $\alpha$ such that

$H+L(\alpha )\geq 0,$

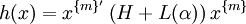meaning that the matrix $H+L(\alpha )$ is positive-semidefinite. This is a linear matrix inequality (LMI) feasibility test, which is a convex optimization problem. The expression $h(x)=x^{{\{m\}'}}\left(H+L(\alpha )\right)x^{{\{m\}}}$ was introduced in [1] with the name square matricial representation (SMR) in order to establish whether a form is SOS via an LMI. This representation is also known as Gram matrix (see [2] and references therein).

Examples

Consider the form of degree 4 in two variables 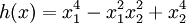$h(x)=x_{1}^{4}-x_{1}^{2}x_{2}^{2}+x_{2}^{4}$ . We have
$m=2,~x^{{\{m\}}}=\left({\begin{array}{c}x_{1}^{2}\\x_{1}x_{2}\\x_{2}^{2}\end{array}}\right),~H+L(\alpha )=\left({\begin{array}{ccc}1&0&-\alpha _{1}\\0&-1+2\alpha _{1}&0\\-\alpha _{1}&0&1\end{array}}\right).$

Since there exists α such that 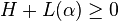$H+L(\alpha )\geq 0$ , namely 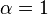$\alpha =1$ , it follows that h(x) is SOS.
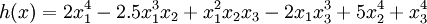Consider the form of degree 4 in three variables $h(x)=2x_{1}^{4}-2.5x_{1}^{3}x_{2}+x_{1}^{2}x_{2}x_{3}-2x_{1}x_{3}^{3}+5x_{2}^{4}+x_{3}^{4}$ . We have
$m=2,~x^{{\{m\}}}=\left({\begin{array}{c}x_{1}^{2}\\x_{1}x_{2}\\x_{1}x_{3}\\x_{2}^{2}\\x_{2}x_{3}\\x_{3}^{2}\end{array}}\right),~H+L(\alpha )=\left({\begin{array}{cccccc}2&-1.25&0&-\alpha _{1}&-\alpha _{2}&-\alpha _{3}\\-1.25&2\alpha _{1}&0.5+\alpha _{2}&0&-\alpha _{4}&-\alpha _{5}\\0&0.5+\alpha _{2}&2\alpha _{3}&\alpha _{4}&\alpha _{5}&-1\\-\alpha _{1}&0&\alpha _{4}&5&0&-\alpha _{6}\\-\alpha _{2}&-\alpha _{4}&\alpha _{5}&0&2\alpha _{6}&0\\-\alpha _{3}&-\alpha _{5}&-1&-\alpha _{6}&0&1\end{array}}\right).$

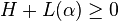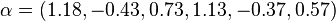Since $H+L(\alpha )\geq 0$ for $\alpha =(1.18,-0.43,0.73,1.13,-0.37,0.57)$ , it follows that h(x) is SOS.

Matrix SOS

A matrix form F(x) (i.e., a matrix whose entries are forms) of dimension r and degree 2m in the real n-dimensional vector x is SOS if and only if there exist matrix forms $G_{1}(x),\ldots ,G_{k}(x)$ of degree m such that

$F(x)=\sum _{{i=1}}^{k}G_{i}(x)'G_{i}(x).$

Matrix SMR

To establish whether a matrix form F(x) is SOS amounts to solving a convex optimization problem. Indeed, similarly to the scalar case any F(x) can be written according to the SMR as

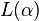$F(x)=\left(x^{{\{m\}}}\otimes I_{r}\right)'\left(H+L(\alpha )\right)\left(x^{{\{m\}}}\otimes I_{r}\right)$

where $\otimes$ is the Kronecker product of matrices, H is any symmetric matrix satisfying

$F(x)=\left(x^{{\{m\}}}\otimes I_{r}\right)'H\left(x^{{\{m\}}}\otimes I_{r}\right)$

and $L(\alpha )$ is a linear parameterization of the linear space

${\mathcal {L}}=\left\{L=L':~\left(x^{{\{m\}}}\otimes I_{r}\right)'L\left(x^{{\{m\}}}\otimes I_{r}\right)=0\right\}.$

The dimension of the vector $\alpha$ is given by

$\omega (n,2m,r)={\frac {1}{2}}r\left(\sigma (n,m)\left(r\sigma (n,m)+1\right)-(r+1)\sigma (n,2m)\right).$

Then, F(x) is SOS if and only if there exists a vector $\alpha$ such that the following LMI holds:

$H+L(\alpha )\geq 0.$

The expression $F(x)=\left(x^{{\{m\}}}\otimes I_{r}\right)'\left(H+L(\alpha )\right)\left(x^{{\{m\}}}\otimes I_{r}\right)$ was introduced in [3] in order to establish whether a matrix form is SOS via an LMI.

References

[1] G. Chesi, A. Tesi, A. Vicino, and R. Genesio, On convexification of some minimum distance problems, 5th European Control Conference, Karlsruhe (Germany), 1999.

[2] M. Choi, T. Lam, and B. Reznick, Sums of squares of real polynomials, in Proc. of Symposia in Pure Mathematics, 1995.

[3] G. Chesi, A. Garulli, A. Tesi, and A. Vicino, Robust stability for polytopic systems via polynomially parameter-dependent Lyapunov functions, in 42nd IEEE Conference on Decision and Control, Maui (Hawaii), 2003.

Notes

↑ , .
↑ .

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.