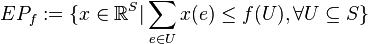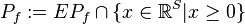Polymatroid
From Wikipedia, the free encyclopedia
In mathematics, polymatroid is a polytope associated with a submodular function. The notion was introduced by Jack Edmonds in 1970.[1]
Definition
Consider any submodular set function  on
on 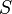 . Then define two associated polyhedra.
. Then define two associated polyhedra.
Here 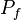 is called the polymatroid and
is called the polymatroid and 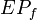 is called the extended polymatroid associated with
is called the extended polymatroid associated with  .[2]
.[2]
Properties
-
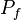 is nonempty if and only if
is nonempty if and only if  and that
and that 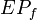 is nonempty if and only if
is nonempty if and only if 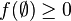
- Given any extended polymatroid
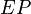 there is a unique submodular function
there is a unique submodular function  such that
such that 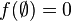 and
and 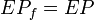
- If r is integral, 1-Lipschitz, and
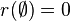 then r is the rank-function of a matroid, and the polymatroid is the independent set polytope, so-called since Edmonds showed it is the convex hull of the characteristic vectors of all independent sets of the matroid.
then r is the rank-function of a matroid, and the polymatroid is the independent set polytope, so-called since Edmonds showed it is the convex hull of the characteristic vectors of all independent sets of the matroid. - For a supermodular f one analogously may define the contrapolymatroid

- This analogously generalizes the dominant of the spanning set polytope of matroids.
Citations
<div class="reflist columns references-column-width" style="-moz-column-width: [1]; -webkit-column-width: [1]; column-width: [1]; list-style-type: decimal;">
- ↑ 1.0 1.1 1.2 1.3 Edmonds, Jack. Submodular functions, matroids, and certain polyhedra. 1970. Combinatorial Structures and their Applications (Proc. Calgary Internat. Conf., Calgary, Alta., 1969) pp. 69–87 Gordon and Breach, New York. MR 0270945
- ↑ (Schrijver 2003, §44, p. 767)
References
General References
- Schrijver, Alexander (2003), Combinatorial Optimization, Springer, ISBN 3-540-44389-4
- Lee, Jon (2004), A First Course in Combinatorial Optimization, Cambridge University Press, ISBN 0-521-01012-8
- Fujishige, Saruto (2005), Submodular Functions and Optimization, Elsevier, ISBN 0-444-52086-4
- Narayanan, H. (1997), Submodular Functions and Electrical Networks, ISBN 0-444-82523-1
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.