Polar set

From Wikipedia, the free encyclopedia

See also polar set (potential theory).

In functional analysis and related areas of mathematics the polar set of a given subset of a vector space is a certain set in the dual space.

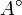Given a dual pair $(X,Y)$ the polar set or polar of a subset $A$ of $X$ is a set $A^{\circ }$ in $Y$ defined as

$A^{\circ }:=\{y\in Y:\sup _{{x\in A}}|\langle x,y\rangle |\leq 1\}$

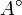The bipolar of a subset $A$ of $X$ is the polar of $A^{\circ }$ . It is denoted 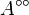$A^{{\circ \circ }}$ and is a set in $X$ .

Properties

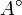$A^{\circ }$ is absolutely convex
If 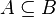$A\subseteq B$ then $B^{\circ }\subseteq A^{\circ }$
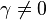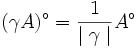
For all $\gamma \neq 0$ : $(\gamma A)^{\circ }={\frac {1}{\mid \gamma \mid }}A^{\circ }$
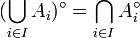
$(\bigcup _{{i\in I}}A_{i})^{\circ }=\bigcap _{{i\in I}}A_{i}^{\circ }$
For a dual pair 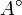$(X,Y)$ $A^{\circ }$ is closed in $Y$ under the weak-*-topology on $Y$
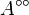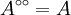The bipolar $A^{{\circ \circ }}$ of a set $A$ is the absolutely convex envelope of $A$ , that is the smallest absolutely convex set containing $A$ . If $A$ is already absolutely convex then $A^{{\circ \circ }}=A$ .
For a closed convex cone $C$ in $X$ , the polar cone is equivalent to the one-sided polar set for $C$ , given by

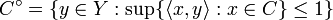$C^{\circ }=\{y\in Y:\sup\{\langle x,y\rangle :x\in C\}\leq 1\}$ .^[1]

Geometry

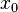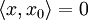In geometry, the polar set may also refer to a duality between points and planes. In particular, the polar set of a point $x_{0}$ , given by the set of points $x$ satisfying $\langle x,x_{0}\rangle =0$ is its polar hyperplane, and the dual relationship for a hyperplane yields its pole.

References

↑ Aliprantis, C.D.; Border, K.C. (2007). Infinite Dimensional Analysis: A Hitchhiker's Guide (3 ed.). Springer. p. 215. doi:10.1007/3-540-29587-9. ISBN 978-3-540-32696-0.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.