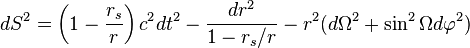Planck length
| SI units | |
|---|---|
| 16.162×10−36 m | 16.162×10−27 nm |
| Natural units | |
| 11.706 ℓS | 305.42×10−27 a0 |
| US customary / Imperial units | |
| 53.025×10−36 ft | 636.30×10−36 in |
In physics, the Planck length, denoted ℓP, is a unit of length, equal to 1.616199(97)×10−35 metres. It is a base unit in the system of Planck units, developed by physicist Max Planck. The Planck length can be defined from three fundamental physical constants: the speed of light in a vacuum, Planck's constant, and the gravitational constant.
Value
The Planck length  is defined as
is defined as
where  is the speed of light in a vacuum,
is the speed of light in a vacuum,  is the gravitational constant, and
is the gravitational constant, and  is the reduced Planck constant. The two digits enclosed by parentheses are the estimated standard error associated with the reported numerical value.[1][2]
is the reduced Planck constant. The two digits enclosed by parentheses are the estimated standard error associated with the reported numerical value.[1][2]
The Planck length is about 10−20 times the diameter of a proton, and thus is exceedingly small.
Theoretical significance
There is currently no proven physical significance of the Planck length; it is, however, a topic of theoretical research. Since the Planck length is so many orders of magnitude smaller than any current instrument could possibly measure, there is no way of examining it directly. According to the generalized uncertainty principle (a concept from speculative models of quantum gravity), the Planck length is, in principle, within a factor of order unity, the shortest measurable length – and no improvement in measurement instruments could change that.
Physical meaning of the Planck length can be determined as follows:
A particle of mass  has a reduced Compton wavelength
has a reduced Compton wavelength
Schwarzschild radius of the particle is
The product of these values is always constant and equal to
Accordingly, the uncertainty relation between the Schwarzschild radius of the particle and Compton wavelength of the particle will have the form
which is another form of Heisenberg's uncertainty principle at the Planck scale. Indeed, substituting the expression for the Schwarzschild radius, we obtain
Reducing the same characters, we come to the Heisenberg uncertainty relation
Uncertainty relation between the gravitational radius and the Compton wavelength of the particle is a special case of the general Heisenberg's uncertainty principle at the Planck scale
where  - the radius of curvature of space-time small domain;
- the radius of curvature of space-time small domain;  - coordinate small domain.
- coordinate small domain.
Indeed, these uncertainty relations can be obtained on the basis of Einstein's equations
where 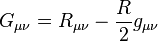 — the Einstein tensor, which combines the Ricci tensor, the scalar curvature and the metric tensor,
— the Einstein tensor, which combines the Ricci tensor, the scalar curvature and the metric tensor,  — the cosmological constant, а
— the cosmological constant, а  energy-momentum tensor of matter,
energy-momentum tensor of matter,  — the number,
— the number,  — the speed of light,
— the speed of light,  — Newton's gravitational constant.
— Newton's gravitational constant.
In the derivation of his equations, Einstein suggested that physical space-time is Riemannian, ie curved. A small domain of it is approximately flat space-time.
For any tensor field  value
value  we may call a tensor density, where
we may call a tensor density, where  - determinant of the metric tensor
- determinant of the metric tensor 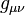 . The integral
. The integral  is a tensor if the domain of integration is small. It is not a tensor if the domain of integration is not small, because it then consists of a sum of tensors located at different points and it does not transform in any simple way under a transformation of coordinates.[3] Here we consider only small domains. This is also true for the integration over the three-dimensional hypersurface
is a tensor if the domain of integration is small. It is not a tensor if the domain of integration is not small, because it then consists of a sum of tensors located at different points and it does not transform in any simple way under a transformation of coordinates.[3] Here we consider only small domains. This is also true for the integration over the three-dimensional hypersurface 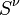 .
.
Thus, Einstein's equations for small space-time domain can be integrated by the three-dimensional hypersurface 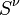 . Have[4]
. Have[4]
Since integrable space-time domain is small, we obtain the tensor equation
where  - 4-momentum,
- 4-momentum,  -
the radius of curvature domain.
-
the radius of curvature domain.
The resulting tensor equation can be rewritten in another form. Since  then
then
where  - the Schwarzschild radius,
- the Schwarzschild radius,  - 4-speed,
- 4-speed,  - gravitational mass. This record reveals the physical meaning of
- gravitational mass. This record reveals the physical meaning of  .
.
In a small area of space-time is almost flat and this equation can be written in the operator form
Then commutator operators  and
and 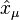 is
is
From here follow the specified uncertainty relations
Substituting the values of 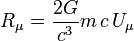 and
and 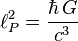 and cutting right and left of the same symbols, we obtain the Heisenberg uncertainty principle
and cutting right and left of the same symbols, we obtain the Heisenberg uncertainty principle
In the particular case of a static spherically symmetric field and static distribution of matter  and have remained
and have remained
where  - the Schwarzschild radius,
- the Schwarzschild radius,  - radial coordinate.
- radial coordinate.
Last uncertainty relation allows make us some estimates of the equations of general relativity at the Planck scale. For example, the equation for the invariant interval 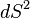 в in the Schwarzschild solution has the form
в in the Schwarzschild solution has the form
Substitute according to the uncertainty relations  . We obtain
. We obtain
It is seen that at the Planck scale 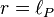 space-time metric is bounded below by the Planck length, and on this scale, there are real and virtual Planckian black holes.
space-time metric is bounded below by the Planck length, and on this scale, there are real and virtual Planckian black holes.
Similar estimates can be made in other equations of general relativity. For example, analysis of the Hamilton-Jacobi equation for a centrally symmetric gravitational field in spaces of different dimensions (with help of the resulting uncertainty relation) indicates a preference for three-dimensional space for the emergence of virtual black holes (quantum foam).
Prescribed above uncertainty relation valid for strong gravitational fields, as in any sufficiently small domain of a strong field space-time is essentially flat.
This implies that the Planck scale is the limit below which the very notions of space and length cease to exist. Any attempt to investigate the possible existence of shorter distances (less than 1,6 ×10−35 m), by performing higher-energy collisions, would inevitably result in black hole production. Higher-energy collisions, rather than splitting matter into finer pieces, would simply produce bigger black holes.[5] Reduction of the Compton wavelength of the particle increases the Schwarzschild radius. The resulting uncertainty relation generates at the Planck scale virtual black holes.
In some forms of quantum gravity, the Planck length is the length scale at which the structure of spacetime becomes dominated by quantum effects, and it is impossible to determine the difference between two locations less than one Planck length apart. The precise effects of quantum gravity are unknown; it is often guessed that spacetime might have a discrete or foamy structure at a Planck length scale.[citation needed]
The Planck area, equal to the square of the Planck length, plays a role in black hole entropy. The value of this entropy, in units of the Boltzmann constant, is known to be given by  , where
, where  is the area of the event horizon. The Planck area is the area by which a spherical black hole increases when the black hole swallows one bit of information, as was proven by Jacob Bekenstein.[6]
is the area of the event horizon. The Planck area is the area by which a spherical black hole increases when the black hole swallows one bit of information, as was proven by Jacob Bekenstein.[6]
If large extra dimensions exist, the measured strength of gravity may be much smaller than its true (small-scale) value. In this case the Planck length would have no fundamental physical significance, and quantum gravitational effects would appear at other scales.
In string theory, the Planck length is the order of magnitude of the oscillating strings that form elementary particles, and shorter lengths do not make physical sense.[7]
In loop quantum gravity, area is quantized, and the Planck area is, within a factor of order unity, the smallest possible area value.
In doubly special relativity, the Planck length is observer-invariant.
The search for the laws of physics valid at the Planck length is a part of the search for the theory of everything.
Visualization
The size of the Planck length can be visualized as follows: if a particle or dot about 0.1mm in size (which is at or near the smallest the unaided human eye can see) were magnified in size to be as large as the observable universe, then inside that universe-sized "dot", the Planck length would be roughly the size of an actual 0.1mm dot. In other words, the diameter of the observable universe is to within less than an order of magnitude, larger than a 0.1 millimeter object, roughly at or near the limits of the unaided human eye, by about the same factor (10^31) as that 0.1mm object or dot is larger than the Planck length. More simply - on a logarithmic scale, a dot is halfway between the Planck length and the size of the universe.
See also
- Fock–Lorentz symmetry
- Orders of magnitude (length)
- Planck energy
- Planck mass
- Planck epoch
- Planck scale
- Planck temperature
- Planck time
Notes and references
- ↑ John Baez, The Planck Length
- ↑ NIST, "Planck length", NIST's published CODATA constants
- ↑ P.A.M.Dirac(1975), General Theory of Relativity, A Wilay Interscience Publication, p.37
- ↑ A.P.Klimets(2012) "Postigaja mirozdanie", LAP LAMBERT Academic Publishing, Deutschland
- ↑ Bernard J.Carr; Steven B.Giddings (May 2005). "Quantum Black Holes". (Scientific American, Inc.) p.55
- ↑ "Phys. Rev. D 7, 2333 (1973): Black Holes and Entropy". Prd.aps.org. Retrieved 2013-10-21.
- ↑ Cliff Burgess; Fernando Quevedo (November 2007). "The Great Cosmic Roller-Coaster Ride". Scientific American (print) (Scientific American, Inc.). p. 55.
Bibliography
- Garay, Luis J. (January 1995). "Quantum gravity and minimum length". International Journal of Modern Physics A 10 (2): 145 ff. arXiv:arXiv:gr-qc/9403008v2. Bibcode:1995IJMPA..10..145G. doi:10.1142/S0217751X95000085.
External links
- Bowley, Roger; Eaves, Laurence (2010). "Planck Length". Sixty Symbols. Brady Haran for the University of Nottingham.
| ||||||||
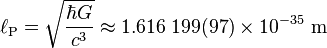
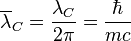
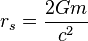
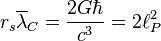





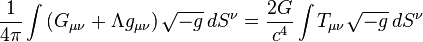



![[{\hat R}_{{\mu }},{\hat x}_{{\mu }}]=-2i\ell _{{P}}^{2}](/2014-wikipedia_en_all_02_2014/I/media/2/6/a/b/26abbc06779962107f5975ec74985669.png)