Planck charge

From Wikipedia, the free encyclopedia

In physics, the Planck charge, denoted by 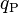$q_{{\text{P}}}$ , is one of the base units in the system of natural units called Planck units. It is a quantity of electric charge defined in terms of fundamental physical constants.

The Planck charge is defined as:^[1] ^[2]

$q_{{\text{P}}}={\sqrt {4\pi \epsilon _{0}\hbar c}}={\sqrt {2ch\epsilon _{0}}}={\frac {e}{{\sqrt {\alpha }}}}=1.875\;5459\times 10^{{-18}}$ coulombs,

where:

$c\$ is the speed of light in the vacuum,

$h\$ is Planck's constant,

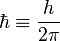$\hbar \equiv {\frac {h}{2\pi }}\$ is the reduced Planck constant,

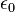$\epsilon _{0}\$ is the permittivity of free space

$e\$ is the elementary charge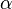

$\alpha \$ = (137.03599911)⁻¹ is the fine structure constant.

The Planck charge is 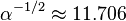$\alpha ^{{-1/2}}\approx 11.706$ times greater than the elementary charge e carried by an electron.

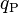The Gaussian cgs units are defined so that $4\pi \epsilon _{0}=1$ , in which case $q_{{\text{P}}}$ has the following simple form:

$q_{{\text{P}}}={\sqrt {\hbar c}}.$

It is customary in theoretical physics to adopt the Lorentz–Heaviside units (also known as rationalized cgs). When made natural ( $c=1$ ) they are like the SI system with $\epsilon _{0}=\mu _{0}=1$ . Therefore it is more appropriate to define the Planck charge as

$q'_{{\text{P}}}={\sqrt {\epsilon _{0}\hbar c}}={\frac {e}{{\sqrt {4\pi \alpha }}}}=5.291\times 10^{{-19}}$ coulombs,

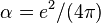When charges are measured in units of $q'_{{\text{P}}}$ , i.e., when $q'_{{\text{P}}}$ is set equal to 1, we obtain $\alpha =e^{2}/(4\pi )$ , which is commonly used in theoretical physics. In contrast, in (non-rationalized) natural cgs units where 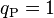$q_{{\text{P}}}=1$ we have $\alpha =e^{2}$ .

Notes and references

↑ Stock, Michael; Witt, Thomas J (2006). "CPEM 2006 round table discussion 'Proposed changes to the SI'". Metrologia 43 (6): 583. Bibcode:2006Metro..43..583S. doi:10.1088/0026-1394/43/6/014.
↑ Pavšič, Matej (2001). The Landscape of Theoretical Physics: A Global View. Dordrecht: Kluwer Academic. pp. 347–352. ISBN 0-7923-7006-6.

v t e Planck's natural units

Base Planck units	Planck time Planck length Planck mass Planck charge Planck temperature

Derived Planck units	Planck energy Planck force Planck power Planck density Planck angular frequency Planck pressure Planck current Planck voltage Planck impedance Planck momentum Planck area Planck volume

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.

Planck charge

See also

Notes and references