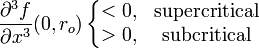Pitchfork bifurcation
In bifurcation theory, a field within mathematics, a pitchfork bifurcation is a particular type of local bifurcation. Pitchfork bifurcations, like Hopf bifurcations have two types - supercritical or subcritical.
In continuous dynamical systems described by ODEs—i.e. flows—pitchfork bifurcations occur generically in systems with symmetry.
Supercritical case

The normal form of the supercritical pitchfork bifurcation is
For negative values of  , there is one stable equilibrium at
, there is one stable equilibrium at  . For
. For  there is an unstable equilibrium at
there is an unstable equilibrium at  , and two stable equilibria at
, and two stable equilibria at 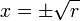 .
.
Subcritical case

The normal form for the subcritical case is
In this case, for  the equilibrium at
the equilibrium at  is stable, and there are two unstable equilbria at
is stable, and there are two unstable equilbria at 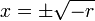 . For
. For  the equilibrium at
the equilibrium at  is unstable.
is unstable.
Formal definition
An ODE
described by a one parameter function 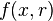 with
with 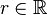 satisfying:
satisfying:
 (f is an odd function),
(f is an odd function),
has a pitchfork bifurcation at  . The form of the pitchfork is given
by the sign of the third derivative:
. The form of the pitchfork is given
by the sign of the third derivative:
References
- Steven Strogatz, "Non-linear Dynamics and Chaos: With applications to Physics, Biology, Chemistry and Engineering", Perseus Books, 2000.
- S. Wiggins, "Introduction to Applied Nonlinear Dynamical Systems and Chaos", Springer-Verlag, 1990.
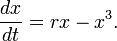
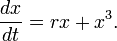
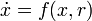
![{\begin{array}{lll}\displaystyle {\frac {\partial f}{\partial x}}(0,r_{{o}})=0,&\displaystyle {\frac {\partial ^{2}f}{\partial x^{2}}}(0,r_{{o}})=0,&\displaystyle {\frac {\partial ^{3}f}{\partial x^{3}}}(0,r_{{o}})\neq 0,\\[12pt]\displaystyle {\frac {\partial f}{\partial r}}(0,r_{{o}})=0,&\displaystyle {\frac {\partial ^{2}f}{\partial r\partial x}}(0,r_{{o}})\neq 0.\end{array}}](/2014-wikipedia_en_all_02_2014/I/media/5/c/b/2/5cb285a832f1af13d268993fc742ad4d.png)