Pinch point (mathematics)

In geometry, a pinch point or cuspidal point is a type of singular point on an algebraic surface.
The equation for the surface near a pinch point may be put in the form
where [4] denotes terms of degree 4 or more and  is not a square in the ring of functions.
is not a square in the ring of functions.
For example the surface  near the point
near the point  , meaning in coordinates vanishing at that point, has the form above. In fact, if
, meaning in coordinates vanishing at that point, has the form above. In fact, if  and
and 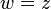 then {
then { } is a system of coordinates vanishing at
} is a system of coordinates vanishing at  then
then  is written in the canonical form.
is written in the canonical form.
The simplest example of a pinch point is the hypersurface defined by the equation 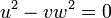 called Whitney umbrella.
called Whitney umbrella.
The pinch point (in this case the origin) is a limit of normal crossings singular points (the  -axis in this case). These singular points are intimately related in the sense that in order to resolve the pinch point singularity one must blow-up the whole
-axis in this case). These singular points are intimately related in the sense that in order to resolve the pinch point singularity one must blow-up the whole  -axis and not only the pinch point.
-axis and not only the pinch point.
See also
References
- P. Griffiths; J. Harris (1994). Principles of Algebraic Geometry. Wiley Classics Library. Wiley Interscience. p. 617. ISBN 0-471-05059-8.
![f(u,v,w)=u^{2}-vw^{2}+[4]\,](/2014-wikipedia_en_all_02_2014/I/media/e/8/2/7/e827dbf7c40a4af2f10356d7bcc92b27.png)