Petrov–Galerkin method
The Petrov–Galerkin method is a mathematical method used to obtain approximate solutions of partial differential equations which contain terms with odd order. In these type of problems a weak formulation with similar function space for test function and solution function is not possible. Hence the method is used in case the test function and solution function belong to different function spaces.[1]
Overview
An example of differential equation containing a term with odd order is as follows:
If a test function  is used to obtain the weak form, the final Galerkin formulation will be given as follows:
is used to obtain the weak form, the final Galerkin formulation will be given as follows:
The term with even order (2nd term in LHS) is now symmetric, as the test function and solution function both have same order of differentiation and they both belong to 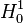 . However, there is no way the first term on LHS can be made this way. In this case the solution space
. However, there is no way the first term on LHS can be made this way. In this case the solution space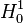 and test function space
and test function space 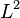 are different and hence the usually employed Bubnov Galerkin method cannot be used.
are different and hence the usually employed Bubnov Galerkin method cannot be used.
In this problem, the formulation method is the same as in the Bubnov-Galerkin method. However the test function and the solution function approximations can not be same, hence they must be approximated separately. As the problem loses symmetry, the final coefficient matrix is also not symmetric and hence the solver selection must be made carefully. These problems sometime pose challenges in terms of computing power and complexity.
See also
- Bubnov-Galerkin method
Notes
- ↑ J. N. Reddy: An introduction to the finite element method, 2006, Mcgraw–Hill
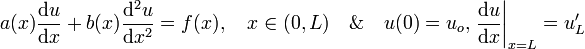
![\int _{0}^{L}a(x)v(x){\dfrac {{\mathrm {d}}u}{{\mathrm {d}}x}}{\mathrm {d}}x-\int _{0}^{L}b(x){\dfrac {{\mathrm {d}}v}{{\mathrm {d}}x}}{\dfrac {{\mathrm {d}}u}{{\mathrm {d}}x}}{\mathrm {d}}x+\left[b(x)v{\dfrac {{\mathrm {d}}u}{{\mathrm {d}}x}}\right]_{0}^{L}=\int _{0}^{L}v(x)f(x)\,{\mathrm {d}}x](/2014-wikipedia_en_all_02_2014/I/media/8/6/2/7/86275d03dbd08980bdf2820dbdb8263b.png)