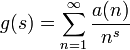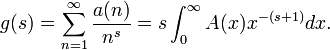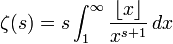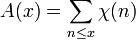Perron's formula

From Wikipedia, the free encyclopedia

In mathematics, and more particularly in analytic number theory, Perron's formula is a formula due to Oskar Perron to calculate the sum of an arithmetical function, by means of an inverse Mellin transform.

Statement

Let 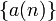$\{a(n)\}$ be an arithmetic function, and let

$g(s)=\sum _{{n=1}}^{{\infty }}{\frac {a(n)}{n^{{s}}}}$

be the corresponding Dirichlet series. Presume the Dirichlet series to be absolutely convergent for 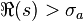$\Re (s)>\sigma _{a}$ . Then Perron's formula is

$A(x)={\sum _{{n\leq x}}}^{{\star }}a(n)={\frac {1}{2\pi i}}\int _{{c-i\infty }}^{{c+i\infty }}g(z){\frac {x^{{z}}}{z}}dz.\;$

Here, the star on the summation indicates that the last term of the sum must be multiplied by 1/2 when x is an integer. The formula requires 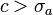$c>\sigma _{a}$ and $x>0$ real, but otherwise arbitrary.

Proof

An easy sketch of the proof comes from taking Abel's sum formula

$g(s)=\sum _{{n=1}}^{{\infty }}{\frac {a(n)}{n^{{s}}}}=s\int _{{0}}^{{\infty }}A(x)x^{{-(s+1)}}dx.$

This is nothing but a Laplace transform under the variable change 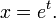$x=e^{t}.$ Inverting it one gets Perron's formula.

Examples

Because of its general relationship to Dirichlet series, the formula is commonly applied to many number-theoretic sums. Thus, for example, one has the famous integral representation for the Riemann zeta function:

$\zeta (s)=s\int _{1}^{\infty }{\frac {\lfloor x\rfloor }{x^{{s+1}}}}\,dx$

and a similar formula for Dirichlet L-functions:

$L(s,\chi )=s\int _{1}^{\infty }{\frac {A(x)}{x^{{s+1}}}}\,dx$

where

$A(x)=\sum _{{n\leq x}}\chi (n)$

and $\chi (n)$ is a Dirichlet character. Other examples appear in the articles on the Mertens function and the von Mangoldt function.

References

Page 243 of Apostol, Tom M. (1976), Introduction to analytic number theory, Undergraduate Texts in Mathematics, New York-Heidelberg: Springer-Verlag, ISBN 978-0-387-90163-3, MR 0434929, Zbl 0335.10001
Weisstein, Eric W., "Perron's formula", MathWorld.
Tenebaum, Gérald (1995). Introduction to analytic and probabilistic number theory. Cambridge: Cambridge University Press. ISBN 0-521-41261-7.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.