Pauling's rules
Pauling's rules are five rules published by Linus Pauling in 1929 for determining the crystal structures of complex ionic crystals.[1] An alternative usage of this phrase refers to rules used to predict the strengths of oxoacids.[2]
First rule
A coordinated polyhedron of anions is formed about each cation, the cation-anion distance determined by the sum of ionic radii and the coordination number (C.N.) by the radius ratio.
The numbers in the table are mathematically derived minimum radius ratios for that geometry. An octahedron may form with a radius ratio greater than or equal to .414, but as the ratio rises above .732, a cubic conformation becomes more stable. These mathematically derived ratios are deviated from in practice; thus, octahedral salt structures with a radius ratio of less than .414 or more than .732 have been observed. If the radius ratio falls below the minimum calculated for ions modeled as spherical balls, it is presumed that the ions are compressed into oblong balls that are not perfect spheres.
| Radius ratio | C.N. | polyhedron |
|---|---|---|
| .225 | 4 | tetrahedron |
| .414 | 6 | octahedron |
| .592 | 7 | capped octahedron |
| .645 | 8 | square antiprism (anticube) |
| .732 | 8 | cube |
| .732 | 9 | triaugmented triangular prism |
| 1.00 | 12 | cuboctahedron |
Second rule: the electrostatic valence rule
An ionic structure will be stable to the extent that the sum of the strengths of the electrostatic bonds that reach an anion equal the charge on that anion.
- i.e. A stable ionic structure must be arranged to preserve Local Electroneutrality.
This is expressed mathematically as:
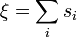
- where
is the charge of the anion and the summation is over the adjacent cations.
Some examples are:
| Cation | Radius ratio | CN | Electrostatic bond strength |
|---|---|---|---|
| Li+ | 0.34 | 4 | 0.25 |
| Mg2+ | 0.47 | 6 | 0.33 |
| Sc3+ | 0.60 | 6 | 0.5 |
Third rule
The sharing of edges and particularly faces by two anion polyhedra decreases the stability of an ionic structure. Sharing of corners does not decrease stability as much, so (for example) octahedra may share corners with one another.
- Effect is largest for cations with high charge and low C.N. (especially when r+/r- approaches the lower limit of the polyhedral stability).
Fourth rule
In a crystal containing different cations, those of high valency and small coordination number tend not to share polyhedron elements with one another.
Fifth rule: the rule of parsimony
The number of essentially different kinds of constituents in a crystal tends to be small. The repeating units will tend to be identical because each atom in the structure is most stable in a specific environment. There may be two or three types of polyhedra, such as tetrahedra or octahedra, but there will not be many different types.
Alternative rules
"Pauling's rules" can also refer to two rules used in predicting the strengths of oxoacids.[3]
1. For the oxoacid OpE(OH)q, pKa ≈ 8 – 5p.
2. The successive pKa values of polyprotic acids (those with q > 1), increase by 5 units for each successive proton transfer.
References
- ↑ Pauling, Linus (1929). "The principles determining the structure of complex ionic crystals". J. Am. Chem. Soc. 51 (4): 1010–1026. doi:10.1021/ja01379a006.
- ↑ Atkins, P.W (2010). Inorganic Chemistry, Fifth Edition. Oxford University Press. p. 125. ISBN 978-1-42-921820-7.
- ↑ Atkins, P.W (2010). Inorganic Chemistry, Fifth Edition. Oxford University Press. p. 125. ISBN 978-1-42-921820-7.