Pauli group

From Wikipedia, the free encyclopedia

The Möbius–Kantor graph, the Cayley graph of the Pauli group $G_{1}$ with generators X, Y, and Z

In physics and mathematics, the Pauli group $G_{1}$ on 1 qubit is the 16-element matrix group consisting of the 2 × 2 identity matrix $I$ and all of the Pauli matrices

$X=\sigma _{1}={\begin{pmatrix}0&1\\1&0\end{pmatrix}},\quad Y=\sigma _{2}={\begin{pmatrix}0&-i\\i&0\end{pmatrix}},\quad Z=\sigma _{3}={\begin{pmatrix}1&0\\0&-1\end{pmatrix}}$ ,

together with the products of these matrices with the factors $-1$ and $\pm i$ :

$G_{1}\ {\stackrel {{\mathrm {def}}}{=}}\ \{\pm I,\pm iI,\pm X,\pm iX,\pm Y,\pm iY,\pm Z,\pm iZ\}\equiv \langle X,Y,Z\rangle$ .

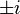The Pauli group is generated by the Pauli matrices, and like them it is named after Wolfgang Pauli.

The Pauli group on n qubits, $G_{n}$ , is the group generated by the operators described above applied to each of $n$ qubits in the tensor product Hilbert space $({\mathbb {C}}^{2})^{{\otimes n}}$ .

References

Nielsen, Michael A; Chuang, Isaac L (2000). Quantum Computation and Quantum Information. Cambridge; New York: Cambridge University Press. ISBN 978-0-521-63235-5. OCLC 43641333. Cite uses deprecated parameters (help)

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.