Path graph
| Path graph | |
|---|---|
|
A path graph on 6 vertices | |
| Vertices | n |
| Edges | n - 1 |
| Radius | ⌊n/2⌋ |
| Diameter | n - 1 |
| Automorphisms | 2 |
| Chromatic number | 2 |
| Chromatic index | 2 |
| Spectrum | {2 cos(k π / (n + 1))1; k=1,...,n} |
| Properties |
Unit distance Bipartite graph Tree |
| Notation |
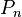 |
In the mathematical field of graph theory, a path graph or linear graph is a particularly simple example of a tree, namely a tree with two or more vertices that is not branched at all, that is, contains only vertices of degree 2 and 1. In particular, it has two terminal vertices (vertices that have degree 1), while all others (if any) have degree 2.
A path in a graph is a sequence of vertices such that from each of its vertices there is an edge to the next vertex in the sequence. A path may be infinite, but a finite path always has a first vertex, called its start vertex, and a last vertex, called its end vertex. Both of them are called end or terminal vertices of the path. The other vertices in the path are internal vertices. A cycle is a path such that the start vertex and end vertex are the same. Note that the choice of the start vertex in a cycle is arbitrary.

Paths and cycles are fundamental concepts of graph theory, described in the introductory sections of most graph theory texts. See e.g. Bondy and Murty (1976), Gibbons (1985), or Diestel (2005). Korte et al. (1990) cover more advanced algorithmic topics concerning paths in graphs.
Different types of path graphs
The same concepts apply both to undirected graphs and directed graphs, with the edges being directed from each vertex to the following one. Often the terms directed path and directed cycle are used in the directed case.
A path with no repeated vertices is called a simple path, and a cycle with no repeated vertices or edges aside from the necessary repetition of the start and end vertex is a simple cycle. In modern graph theory, most often "simple" is implied; i.e., "cycle" means "simple cycle" and "path" means "simple path", but this convention is not always observed, especially in applied graph theory. Some authors (e.g. Bondy and Murty 1976) use the term "walk" for a path in which vertices or edges may be repeated, and reserve the term "path" for what is here called a simple path.
A path such that no graph edges connect two nonconsecutive path vertices is called an induced path.
A simple cycle that includes every vertex, without repetition, of the graph is known as a Hamiltonian cycle.
A cycle with just one edge removed in the corresponding spanning tree of the original graph is known as a Fundamental cycle.
Two paths are independent (alternatively, internally vertex-disjoint) if they do not have any internal vertex in common.
The length of a path is the number of edges that the path uses, counting multiple edges multiple times. The length can be zero for the case of a single vertex.
A weighted graph associates a value (weight) with every edge in the graph. The weight of a path in a weighted graph is the sum of the weights of the traversed edges. Sometimes the words cost or length are used instead of weight.
See also
- Glossary of graph theory
- Shortest path problem
- Traveling salesman problem
- Cycle space
- Path (graph theory)
- Caterpillar tree
- Cycle graph
- Complete graph
- Null graph
- Path decomposition
References
- Bondy, J. A.; Murty, U. S. R. (1976). Graph Theory with Applications. North Holland. pp. 12–21. ISBN 0-444-19451-7.
- Diestel, Reinhard (2005). Graph Theory (3rd ed. ed.). Graduate Texts in Mathematics, vol. 173, Springer-Verlag. pp. 6–9. ISBN 3-540-26182-6.
- Gibbons, A. (1985). Algorithmic Graph Theory. Cambridge University Press. pp. 5–6. ISBN 0-521-28881-9.
- Korte, Bernhard; Lovász, László; Prömel, Hans Jürgen; Schrijver, Alexander (Eds.) (1990). Paths, Flows, and VLSI-Layout. Algorithms and Combinatorics 9, Springer-Verlag. ISBN 0-387-52685-4.
External links