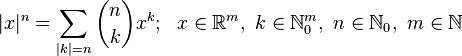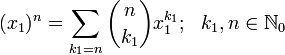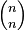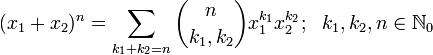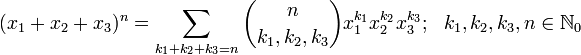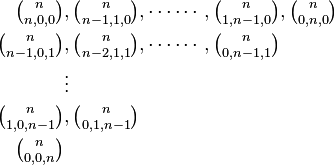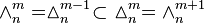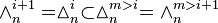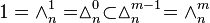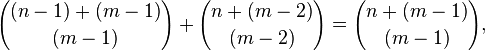Pascal's simplex

From Wikipedia, the free encyclopedia

In mathematics, Pascal's simplex is a generalisation of Pascal's triangle into arbitrary number of dimensions, based on the multinomial theorem.

Generic Pascal's m-simplex

Let m (m > 0) be a number of terms of a polynomial and n (n ≥ 0) be a power the polynomial is raised to.

Let 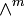\wedge ^{m} denote a Pascal's m-simplex. Each Pascal's m-simplex is a semi-infinite object, which consists of an infinite series of its components.

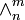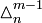Let \wedge _{n}^{m} denote its nth component, itself a finite (m − 1)-simplex with the edge length n, with a notational equivalent \vartriangle _{n}^{{m-1}}.

nth component

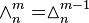\wedge _{n}^{m}=\vartriangle _{n}^{{m-1}} consists of the coefficients of multinomial expansion of a polynomial with m terms raised to the power of n:

|x|^{n}=\sum _{{|k|=n}}{{\binom {n}{k}}x^{k}};\ \ x\in {\mathbb {R}}^{m},\ k\in {\mathbb {N}}_{0}^{m},\ n\in {\mathbb {N}}_{0},\ m\in {\mathbb {N}}

where \textstyle |x|=\sum _{{i=1}}^{m}{x_{i}},\ |k|=\sum _{{i=1}}^{m}{k_{i}},\ x^{k}=\prod _{{i=1}}^{m}{x_{i}^{{k_{i}}}}.

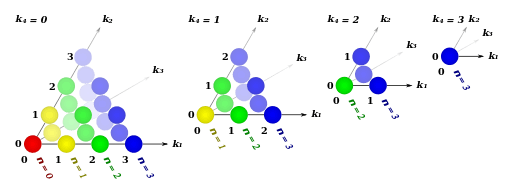
Example for \wedge ^{4}

Pascal's 4-simplex (sequence A189225 in OEIS), sliced along the k4. All points of the same color belong to the same n-th component, from red (for n = 0) to blue (for n = 3).

Specific Pascal's simplices

Pascal's 1-simplex

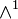\wedge ^{1} is not known by any special name.

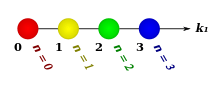
nth component

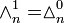\wedge _{n}^{1}=\vartriangle _{n}^{0} (a point) is the coefficient of multinomial expansion of a polynomial with 1 term raised to the power of n:

(x_{1})^{n}=\sum _{{k_{1}=n}}{n \choose k_{1}}x_{1}^{{k_{1}}};\ \ k_{1},n\in {\mathbb {N}}_{0}
Arrangement of 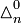\vartriangle _{n}^{0}
\textstyle {n \choose n}

which equals 1 for all n.

Pascal's 2-simplex

\wedge ^{2} is known as Pascal's triangle (sequence A007318 in OEIS).

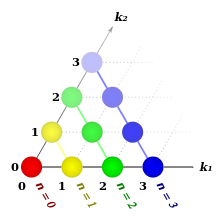
nth component

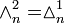\wedge _{n}^{2}=\vartriangle _{n}^{1} (a line) consists of the coefficients of binomial expansion of a polynomial with 2 terms raised to the power of n:

(x_{1}+x_{2})^{n}=\sum _{{k_{1}+k_{2}=n}}{n \choose k_{1},k_{2}}x_{1}^{{k_{1}}}x_{2}^{{k_{2}}};\ \ k_{1},k_{2},n\in {\mathbb {N}}_{0}
Arrangement of 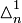\vartriangle _{n}^{1}
\textstyle {n \choose n,0},{n \choose n-1,1},\cdots ,{n \choose 1,n-1},{n \choose 0,n}

Pascal's 3-simplex

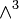\wedge ^{3} is known as Pascal's tetrahedron (sequence A046816 in OEIS).

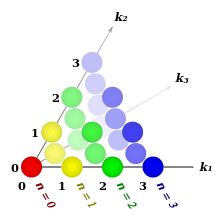
nth component

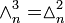\wedge _{n}^{3}=\vartriangle _{n}^{2} (a triangle) consists of the coefficients of trinomial expansion of a polynomial with 3 terms raised to the power of n:

(x_{1}+x_{2}+x_{3})^{n}=\sum _{{k_{1}+k_{2}+k_{3}=n}}{n \choose k_{1},k_{2},k_{3}}x_{1}^{{k_{1}}}x_{2}^{{k_{2}}}x_{3}^{{k_{3}}};\ \ k_{1},k_{2},k_{3},n\in {\mathbb {N}}_{0}
Arrangement of 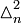\vartriangle _{n}^{2}
{\begin{aligned}\textstyle {n \choose n,0,0}&,\textstyle {n \choose n-1,1,0},\cdots \cdots ,{n \choose 1,n-1,0},{n \choose 0,n,0}\\\textstyle {n \choose n-1,0,1}&,\textstyle {n \choose n-2,1,1},\cdots \cdots ,{n \choose 0,n-1,1}\\&\vdots \\\textstyle {n \choose 1,0,n-1}&,\textstyle {n \choose 0,1,n-1}\\\textstyle {n \choose 0,0,n}\end{aligned}}

Properties

Inheritance of components

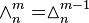\wedge _{n}^{m}=\vartriangle _{n}^{{m-1}} is numerically equal to each (m − 1)-face (there is m + 1 of them) of 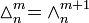\vartriangle _{n}^{m}=\wedge _{n}^{{m+1}}, or:

\wedge _{n}^{m}=\vartriangle _{n}^{{m-1}}\subset \ \vartriangle _{n}^{m}=\wedge _{n}^{{m+1}}

From this follows, that the whole 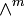\wedge ^{m} is (m + 1)-times included in 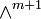\wedge ^{{m+1}}, or:

\wedge ^{m}\subset \wedge ^{{m+1}}

Example 

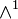
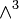
        \wedge ^{1}         \wedge ^{2}        \wedge ^{3}         \wedge ^{4}

\wedge _{0}^{m}     1          1          1          1

\wedge _{1}^{m}     1         1 1        1 1        1 1  1
                              1          1

\wedge _{2}^{m}     1        1 2 1      1 2 1      1 2 1  2 2  1
                             2 2        2 2    2
                              1          1

\wedge _{3}^{m}     1       1 3 3 1    1 3 3 1    1 3 3 1  3 6 3  3 3  1
                            3 6 3      3 6 3    6 6    3
                             3 3        3 3      3
                              1          1

For more terms in the above array refer to (sequence A191358 in OEIS)

Equality of sub-faces

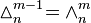Conversely, \wedge _{n}^{{m+1}}=\vartriangle _{n}^{m} is (m + 1)-times bounded by \vartriangle _{n}^{{m-1}}=\wedge _{n}^{m}, or:

\wedge _{n}^{{m+1}}=\vartriangle _{n}^{m}\supset \vartriangle _{n}^{{m-1}}=\wedge _{n}^{m}

From this follows, that for given n, all i-faces are numerically equal in nth components of all Pascal's (m > i)-simplices, or:

\wedge _{n}^{{i+1}}=\vartriangle _{n}^{i}\subset \vartriangle _{n}^{{m>i}}=\wedge _{n}^{{m>i+1}}

Example

The 3rd component (2-simplex) of Pascal's 3-simplex is bounded by 3 equal 1-faces (lines). Each 1-face (line) is bounded by 2 equal 0-faces (vertices):

2-simplex   1-faces of 2-simplex         0-faces of 1-face

 1 3 3 1    1 . . .  . . . 1  1 3 3 1    1 . . .   . . . 1
  3 6 3      3 . .    . . 3    . . .
   3 3        3 .      . 3      . .
    1          1        1        .

Also, for all m and all n:

1=\wedge _{n}^{1}=\vartriangle _{n}^{0}\subset \vartriangle _{n}^{{m-1}}=\wedge _{n}^{m}

Number of coefficients

For the nth component ((m − 1)-simplex) of Pascal's m-simplex, the number of the coefficients of multinomial expansion it consists of is given by:

{(n-1)+(m-1) \choose (m-1)}+{n+(m-2) \choose (m-2)}={n+(m-1) \choose (m-1)},

that is, either by a sum of the number of coefficients of an (n − 1)th component ((m − 1)-simplex) of Pascal's m-simplex with the number of coefficients of an nth component ((m − 2)-simplex) of Pascal's (m − 1)-simplex, or by a number of all possible partitions of an nth power among m exponents.

Example

Number of coefficients of nth component ((m − 1)-simplex) of Pascal's m-simplex
m-simplex nth component n = 0 n = 1 n = 2 n = 3 n = 4 n = 5
1-simplex 0-simplex 1 1 1 1 1 1
2-simplex 1-simplex 1 2 3 4 5 6
3-simplex 2-simplex 1 3 6 10 15 21
4-simplex 3-simplex 1 4 10 20 35 56
5-simplex 4-simplex 1 5 15 35 70 126
6-simplex 5-simplex 1 6 21 56 126 252

Interestingly, the terms of this table comprise a Pascal triangle in the format of a symmetric Pascal matrix.

Symmetry

(An nth component ((m − 1)-simplex) of Pascal's m-simplex has the (m!)-fold spatial symmetry.)

Geometry

(Orthogonal axes k_1 ... k_m in m-dimensional space, vertices of component at n on each axe, the tip at [0,...,0] for n=0.)

Numeric construction

(Wrapped n-th power of a big number gives instantly the n-th component of a Pascal's simplex.)

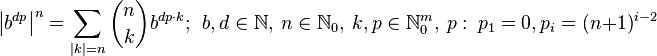
\left|b^{{dp}}\right|^{n}=\sum _{{|k|=n}}{{\binom {n}{k}}b^{{dp\cdot k}}};\ \ b,d\in {\mathbb {N}},\ n\in {\mathbb {N}}_{0},\ k,p\in {\mathbb {N}}_{0}^{m},\ p:\ p_{1}=0,p_{i}=(n+1)^{{i-2}}

where \textstyle b^{{dp}}=(b^{{dp_{1}}},\cdots ,b^{{dp_{m}}})\in {\mathbb {N}}^{m},\ p\cdot k={\sum _{{i=1}}^{m}{p_{i}k_{i}}}\in {\mathbb {N}}_{0}.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.