Partial geometry

From Wikipedia, the free encyclopedia

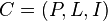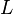An incidence structure $C=(P,L,I)$ consists of points $P$ , lines $L$ , and flags 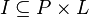$I\subseteq P\times L$ where a point $p$ is said to be incident with a line $l$ if $(p,l)\in I$ . It is a (finite) partial geometry if there are integers $s,t,\alpha \geq 1$ such that:

For any pair of distinct points $p$ and $q$ , there is at most one line incident with both of them.
Each line is incident with $s+1$ points.
Each point is incident with 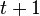$t+1$ lines.
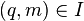If a point $p$ and a line $l$ are not incident, there are exactly $\alpha$ pairs $(q,m)\in I$ , such that $p$ is incident with $m$ and $q$ is incident with $l$ .

A partial geometry with these parameters is denoted by $pg(s,t,\alpha )$ .

Properties

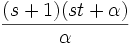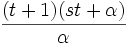The number of points is given by ${\frac {(s+1)(st+\alpha )}{\alpha }}$ and the number of lines by ${\frac {(t+1)(st+\alpha )}{\alpha }}$ .
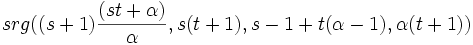The point graph of a $pg(s,t,\alpha )$ is a strongly regular graph : $srg((s+1){\frac {(st+\alpha )}{\alpha }},s(t+1),s-1+t(\alpha -1),\alpha (t+1))$ .
Partial geometries are dual structures : the dual of a $pg(s,t,\alpha )$ is simply a $pg(t,s,\alpha )$ .

Special case

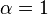The generalized quadrangles are exactly those partial geometries $pg(s,t,\alpha )$ with $\alpha =1$ .

Partial geometry

Properties

Special case

See also