Parikh's theorem

From Wikipedia, the free encyclopedia

Parikh's theorem in theoretical computer science says that if one looks only at the relative number of occurrences of terminal symbols in a context-free language, without regard to their order, then the language is indistinguishable from a regular language.^[1] It is useful for deciding whether or not a string with a given number of some terminals is accepted by a context-free grammar.^[2] It was first proved by Rohit Parikh in 1961^[3] and republished in 1966.^[4]

Definitions and formal statement

Let 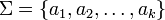$\Sigma =\{a_{1},a_{2},\ldots ,a_{k}\}$ be an alphabet. The Parikh vector of a word is defined as the function $p:\Sigma ^{*}\to {\mathbb {N}}^{k}$ , given by^[1]

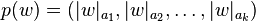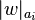$p(w)=(|w|_{{a_{1}}},|w|_{{a_{2}}},\ldots ,|w|_{{a_{k}}})$ , where $|w|_{{a_{i}}}$ denotes the number of occurrences of the letter $a_{i}$ in the word $w$ .

A subset of ${\mathbb {N}}^{k}$ is said to be linear if it is of the form

$u_{0}+\langle u_{1},\ldots ,u_{m}\rangle =\{u_{0}+t_{1}u_{1}+\ldots +t_{m}u_{m}\mid t_{1},\ldots ,t_{m}\in {\mathbb {N}}\}$ for some vectors $u_{0},\ldots ,u_{m}$ .

A subset of ${\mathbb {N}}^{k}$ is said to be semi-linear if it is a union of finitely many linear subsets.

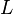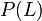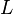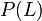The formal statement of Parikh's theorem is as follows. Let $L$ be a context-free language. Let $P(L)$ be the set of Parikh vectors of words in $L$ , that is, $P(L)=\{p(w)\mid w\in L\}$ . Then $P(L)$ is a semi-linear set.

If 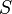$S$ is any semi-linear set, the language of words whose Parikh vectors are in 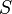$S$ is a regular language. Thus, if one considers two languages to be commutatively equivalent if they have the same set of Parikh vectors, then every context-free language is commutatively equivalent to some regular language.

Significance

Parikh's theorem proves that some context-free languages can only have ambiguous grammars. Such languages are called inherently ambiguous languages. From a formal grammar perspective, this means that some ambiguous context-free grammars cannot be converted to equivalent unambiguous context-free grammars.

References

↑ 1.0 1.1 Kozen, Dexter (1997). Automata and Computability. New York: Springer-Verlag. ISBN 3-540-78105-6.
↑ Håkan Lindqvist. "Parikh's theorem". Umeå Universitet.
↑ Parikh, Rohit (1961). "Language Generating Devices". Quartly Progress Report, Research Laboratory of Electronics, MIT.
↑ Parikh, Rohit (1966). "On Context-Free Languages". Journal of the Association for Computing Machinery 13 (4).

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.