Pareto efficiency

From Wikipedia, the free encyclopedia

Pareto efficiency, or Pareto optimality, is a state of allocation of resources in which it is impossible to make any one individual better off without making at least one individual worse off. The term is named after Vilfredo Pareto (1848–1923), an Italian economist who used the concept in his studies of economic efficiency and income distribution.^{[citation needed]} The concept has applications in academic fields such as economics and engineering.

Given an initial allocation of goods among a set of individuals, a change to a different allocation that makes at least one individual better off without making any other individual worse off is called a Pareto improvement. An allocation is defined as "Pareto efficient" or "Pareto optimal" when no further Pareto improvements can be made.

For example, suppose there are two consumers A & B and only one resource X. Suppose X is equal to 20. Let us assume that the resource has to be distributed equally between A and B and thus can be distributed in the following way: (1,1), (2,2), (3,3), (4,4), (5,5), (6,6), (7,7), (8,8), (9,9), (10,10). At point (10,10) all resources have been exhausted. No further distribution is possible—if redistribution continues, it will lead to a position (11,9) or (9,11) that makes one better off and the other worse off. Hence, point (10,10) is Pareto optimal; no further Pareto improvements can be made.

Pareto efficiency is a minimal notion of efficiency and does not necessarily result in a socially desirable distribution of resources: it makes no statement about equality, or the overall well-being of a society.^[1]^[2] The notion of Pareto efficiency can also be applied to the selection of alternatives in engineering and similar fields. Each option is first assessed under multiple criteria and then a subset of options is identified with the property that no other option can categorically outperform any of its members.

Pareto efficiency in short

This example of a Production-possibility frontier provides a simple example for illustrating Pareto efficiency. Suppose that there are two agents in an economy, guns and one that only values butter. Point A is not Pareto efficient because it is possible to produce more of either one or both goods (Butter and Guns) without producing less of the other. Thus, moving from A to D enables you to make one person better off without making anyone else worse off (Pareto improvement). The locus of the point D is a curve BC, representing the limits of the current production efficiency. However, the curve BC is not in itself Pareto efficient. Moving to point B from point A, is not a Pareto improvement, as less butter is produced. Likewise, moving to point C from point A is not a Pareto improvement, as fewer guns are produced. However, the arc EF, joining points E and F on the frontier curve is Pareto efficient within the achievable limits of current production capacity, with respect to A, i.e., only the arc whose endpoints are created by the lines perpendicular to the co-ordinate axes subtended from the point A and extended to meet the said curve at the respective endpoints, is pareto efficient.

It is commonly accepted that outcomes that are not Pareto efficient are to be avoided, and therefore Pareto efficiency is an important criterion for evaluating economic systems and public policies.^{[citation needed]} If economic allocation in any system is not Pareto efficient, there is potential for a Pareto improvement—an increase in Pareto efficiency: through reallocation, improvements can be made to at least one participant's well-being without reducing any other participant's well-being.

It is important to note, however, that a change from an inefficient allocation to an efficient one is not necessarily a Pareto improvement. Thus, in practice, ensuring that nobody is disadvantaged by a change aimed at achieving Pareto efficiency may require compensation of one or more parties. For instance, if a change in economic policy eliminates a monopoly and that market subsequently becomes competitive and more efficient, the monopolist will be made worse off. However, the loss to the monopolist will be more than offset by the gain in efficiency. This means the monopolist can be compensated for its loss while still leaving a net gain for others in the economy, a Pareto improvement.

In real-world practice, such compensations have unintended consequences. They can lead to incentive distortions over time as agents anticipate such compensations and change their actions accordingly. Under certain idealized conditions, it can be shown that a system of free markets will lead to a Pareto efficient outcome. This is called the first welfare theorem. It was first demonstrated mathematically by economists Kenneth Arrow and Gérard Debreu. However, the result only holds under the restrictive assumptions necessary for the proof (markets exist for all possible goods so there are no externalities, all markets are in full equilibrium, markets are perfectly competitive, transaction costs are negligible, and market participants have perfect information). In the absence of perfect information or complete markets, outcomes will generically be Pareto inefficient, per the Greenwald–Stiglitz theorem.^[3]

Weak Pareto efficiency

A "weak Pareto optimum" (WPO) is an allocation for which there are no possible alternative allocations whose realization would cause every individual to gain. Thus an alternative allocation is considered to be a Pareto improvement only if the alternative allocation is strictly preferred by all individuals. When contrasted with weak Pareto efficiency, a standard Pareto optimum as described above may be referred to as a "strong Pareto optimum" (SPO).

Weak Pareto-optimality is "weaker" than strong Pareto-optimality in the sense that any SPO also qualifies as a WPO, but a WPO allocation is not necessarily an SPO.

Use in engineering

Example of a Pareto frontier. The boxed points represent feasible choices, and smaller values are preferred to larger ones. Point C is not on the Pareto Frontier because it is dominated by both point A and point B. Points A and B are not strictly dominated by any other, and hence do lie on the frontier.

The notion of Pareto efficiency is also useful in engineering. Given a set of choices and a way of valuing them, the Pareto frontier or Pareto set or Pareto front is the set of choices that are Pareto efficient. By restricting attention to the set of choices that are Pareto-efficient, a designer can make tradeoffs within this set, rather than considering the full range of every parameter.

The Pareto frontier is defined formally as follows. Consider a design space with n real parameters (corresponding to the allocation of goods in the economics interpretation), and for each design space point there are m different criteria by which to judge that point (corresponding to the utility of the different agents in the economics interpretation). Let 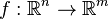$f:{\mathbb {R}}^{n}\rightarrow {\mathbb {R}}^{m}$ be the function which assigns, to each design space point x, a criteria space point f(x). This represents the way of valuing the designs. Now, it may be that some designs are infeasible; so let X be a set of feasible designs in ${{\mathbb {R}}}^{n}$ , which must be a compact set. Then the set which represents the feasible criterion points is f(X), the image of the set X under the action of f. Call this image Y. Now construct the Pareto frontier as a subset of Y of the feasible criterion points. It is often assumed in engineering that the preferable values of each criterion parameter are the lesser ones (e.g. lower emissions or lower cost), thus minimizing each dimension of the criterion vector is desired. 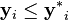Then compare criterion vectors as follows: One criterion vector y strictly dominates (or "is preferred to") a vector y* if each parameter of y is not strictly greater than the corresponding parameter of y* and at least one parameter is strictly less: that is, ${\mathbf {y}}_{i}\leq {\mathbf {y^{*}}}_{i}$ for each i and ${\mathbf {y}}_{i}<{\mathbf {y^{*}}}_{i}$ for some i. 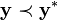This is written as ${\mathbf {y}}\prec {\mathbf {y^{*}}}$ to mean that y strictly dominates y*. Then the Pareto frontier is the set of points from Y that are not strictly dominated by any other point in Y. Formally, this defines a partial order on Y, namely the product order on 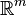${\mathbb {R}}^{m}$ (more precisely, the induced order on Y as a subset of 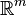${\mathbb {R}}^{m}$ ), and the Pareto frontier is the set of maximal elements with respect to this order.

Algorithms for computing the Pareto frontier of a finite set of alternatives have been studied in computer science, power engineering,^[4] sometimes referred to as the maximum vector problem or the skyline query.^[5]^[6]

References

↑ Barr, Nicholas (2012). "3.2.2 The relevance of efficiency to different theories of society". Economics of the Welfare State (5th ed.). Oxford University Press. p. 46. ISBN 978-0-19-929781-8.
↑ Sen, Amartya (October 1993). "Markets and freedom: Achievements and limitations of the market mechanism in promoting individual freedoms" (PDF). Oxford Economic Papers 45 (4): 519–541. JSTOR 2663703.
↑ Greenwald, Bruce; Stiglitz, Joseph E. (1986). "Externalities in economies with imperfect information and incomplete markets". Quarterly Journal of Economics 101 (2): 229–264. doi:10.2307/1891114. JSTOR 1891114.
↑ Tomoiagă, B.; Chindriş, M.; Sumper, A.; Sudria-Andreu, A.; Villafafila-Robles, R. Pareto Optimal Reconfiguration of Power Distribution Systems Using a Genetic Algorithm Based on NSGA-II. Energies 2013, 6, 1439-1455.
↑ Kung, H.T.; Luccio, F.; Preparata, F.P. (1975). "On finding the maxima of a set of vectors.". Journal of the ACM 22 (4): 469–476. doi:10.1145/321906.321910.
↑ Godfrey, Parke; Shipley, Ryan; Gryz, Jarek (2006). "Algorithms and Analyses for Maximal Vector Computation". VLDB Journal 16: 5–28. doi:10.1007/s00778-006-0029-7

Fudenberg, D.; Tirole, J. (1983). "1.2.4 Multiple Nash Equilibria, Focal Points, and Pareto Optimality". Game Theory. MIT Press. p. 18. ISBN 0-262-06141-4.
Ng, Yew-Kwang (1983). Welfare Economics. Macmillan. ISBN 0-333-97121-3.
Osborne, Martin J.; Rubinstein, Ariel (1994). Course in Game Theory. MIT Press. pp. 6–. ISBN 978-0-262-65040-3.
Mathur, Vijay K. (1991). "How Well Do We Know Pareto Optimality?". Journal of Economic Education 22 (2): 172–8.

v t e Topics in game theory

Definitions	Normal-form game Extensive-form game Graphical game Cooperative game Succinct game Information set Hierarchy of beliefs Preference

Equilibrium concepts	Nash equilibrium Subgame perfection Mertens-stable equilibrium Bayesian-Nash Perfect Bayesian Trembling hand Proper equilibrium Epsilon-equilibrium Correlated equilibrium Sequential equilibrium Quasi-perfect equilibrium Evolutionarily stable strategy Risk dominance Core Shapley value Pareto efficiency Quantal response equilibrium Self-confirming equilibrium Strong Nash equilibrium Markov perfect equilibrium

Strategies	Dominant strategies Pure strategy Mixed strategy Tit for tat Grim trigger Collusion Backward induction Forward induction Markov strategy

Classes of games	Symmetric game Perfect information Simultaneous game Sequential game Repeated game Signaling game Cheap talk Zero-sum game Mechanism design Bargaining problem Stochastic game Large Poisson game Nontransitive game Global games

Games	Prisoner's dilemma Traveler's dilemma Coordination game Chicken Centipede game Volunteer's dilemma Dollar auction Battle of the sexes Stag hunt Matching pennies Ultimatum game Rock-paper-scissors Pirate game Dictator game Public goods game Blotto games War of attrition El Farol Bar problem Cake cutting Cournot game Deadlock Diner's dilemma Guess 2/3 of the average Kuhn poker Nash bargaining game Screening game Prisoners and hats puzzle Trust game Princess and monster game Monty Hall problem

Theorems	Minimax theorem Nash's theorem Purification theorem Folk theorem Revelation principle Arrow's impossibility theorem

Key figures	Kenneth Arrow Robert Aumann Kenneth Binmore Samuel Bowles Melvin Dresher Merrill M. Flood Drew Fudenberg Donald B. Gillies John Harsanyi Leonid Hurwicz David K. Levine Daniel Kahneman Harold W. Kuhn Eric Maskin Jean-François Mertens Paul Milgrom Oskar Morgenstern Roger Myerson John Nash John von Neumann Ariel Rubinstein Thomas Schelling Reinhard Selten Herbert Simon Lloyd Shapley John Maynard Smith Jean Tirole Albert W. Tucker William Vickrey Robert B. Wilson Peyton Young

See also	Tragedy of the commons Tyranny of small decisions All-pay auction List of games in game theory Confrontation analysis List of game theorists Combinatorial game theory

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.

Pareto efficiency

Pareto efficiency in short

Weak Pareto efficiency

Use in engineering

See also

References