Pancyclic graph
In the mathematical study of graph theory, a pancyclic graph is a directed graph or undirected graph that contains cycles of all possible lengths from three up to the number of vertices in the graph.[1] Pancyclic graphs are a generalization of Hamiltonian graphs, graphs which have a cycle of the maximum possible length.
Definitions
An n-vertex graph G is pancyclic if, for every k in the range 3 ≤ k ≤ n, G contains a cycle of length k.[1] It is node-pancyclic or vertex-pancyclic if, for every vertex v and every k in the same range, it contains a cycle of length k that contains v.[2] Similarly, it is edge-pancyclic if, for every edge e and every k in the same range, it contains a cycle of length k that contains e.[2]
A bipartite graph cannot be pancyclic, because it does not contain any odd-length cycles, but it is said to be bipancyclic if it contains cycles of all even lengths from 4 to n.[3]
Planar graphs
A maximal outerplanar graph is a graph formed by a simple polygon in the plane by triangulating its interior. Every maximal outerplanar graph is pancyclic, as can be shown by induction. The outer face of the graph is an n-vertex cycle, and removing any triangle connected to the rest of the graph by only one edge (a leaf of the tree that forms the dual graph of the triangulation) forms a maximal outerplanar graph on one fewer vertex, that by induction has cycles of all the remaining lengths. With more care in choosing which triangle to remove, the same argument shows more strongly that every maximal outerplanar graph is node-pancyclic.[4] The same holds for graphs that have a maximal outerplanar spanning subgraph, as do for instance the wheel graphs.
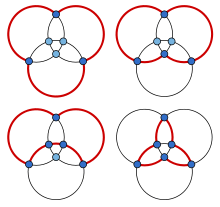
A maximal planar graph is a planar graph in which all faces, even the outer face, are triangles. A maximal planar graph is node-pancyclic if and only if it has a Hamiltonian cycle:[5] if it is not Hamiltonian, it is certainly not pancyclic, and if it is Hamiltonian, then the interior of the Hamiltonian cycle forms a maximal outerplanar graph on the same nodes, to which the previous argument for maximal outerplanar graphs can be applied.[6] For instance, the illustration shows the pancyclicity of the graph of an octahedron, a Hamiltonian maximal planar graph with six vertices. More strongly, by the same argument, if a maximal planar graph has a cycle of length k, it has cycles of all smaller lengths.[7]
Halin graphs are the planar graphs formed from a planar drawing of a tree that has no degree-two vertices, by adding a cycle to the drawing that connects all the leaves of the tree. Halin graphs are not necessarily pancyclic, but they are almost pancyclic in the sense that there is at most one missing cycle length. The length of the missing cycle is necessarily even. If none of the interior vertices of a Halin graph has degree three, then it is necessarily pancyclic.[8]
Bondy (1971) observed that many classical conditions for the existence of a Hamiltonian cycle were also sufficient conditions for a graph to be pancyclic, and on this basis conjectured that every 4-connected planar graph is pancyclic. However, Malkevitch (1971) found a family of counterexamples.
Tournaments
A tournament is a directed graph with one directed edge between each pair of vertices. Intuitively, a tournament can be used to model a round-robin sports competition, by drawing an edge from the winner to the loser of each game in the competition. A tournament is called strongly connected or strong if and only if it cannot be partitioned into two subsets L and W of losers and winners, such that every competitor in W beats every competitor in L.[9] Every strong tournament is pancyclic[10] and node-pancyclic.[11] If a tournament is regular (each competitor has the same number of wins and losses as each other competitor) then it is also edge-pancyclic;[12] however, a strong tournament with four vertices cannot be edge-pancyclic.
Graphs with many edges
Mantel's theorem states that any n-vertex undirected graph with at least n2/4 edges, and no multiple edges or self-loops, either contains a triangle or it is the complete bipartite graph Kn/2,n/2. This theorem can be strengthened: any undirected Hamiltonian graph with at least n2/4 edges is either pancyclic or Kn/2,n/2.[1]
There exist n-vertex Hamiltonian directed graphs with n(n + 1)/2 − 3 edges that are not pancyclic, but every Hamiltonian directed graph with at least n(n + 1)/2 − 1 edges is pancyclic. Additionally, every n-vertex strongly connected graph in which each edge has degree at least n (counting incoming and outgoing edges together) is either pancyclic or it is a complete bipartite graph.[13]
Graph powers
For any graph G, its kth power Gk is defined as the graph on the same vertex set that has an edge between every two vertices whose distance in G is at most k. If G is 2-vertex-connected, then by Fleischner's theorem its square G2 is Hamiltonian; this can be strengthened to show that it is necessarily vertex-pancyclic.[14] More strongly, whenever G2 is Hamiltonian, it is also pancyclic.[15]
Computational complexity
It is NP-complete to test whether a graph is pancyclic, even for the special case of 3-connected cubic graphs, and it is also NP-complete to test whether a graph is node-pancyclic, even for the special case of polyhedral graphs.[16] It is also NP-complete to test whether the square of a graph is Hamiltonian, and therefore whether it is pancyclic.[17]
History
Pancyclicity was first investigated in the context of tournaments by Harary & Moser (1966), Moon (1966), and Alspach (1967). The concept of pancyclicity was named and extended to undirected graphs by Bondy (1971).
Notes
- ↑ 1.0 1.1 1.2 Bondy (1971).
- ↑ 2.0 2.1 Randerath et al. (2002).
- ↑ Schmeichel & Mitchem (1982).
- ↑ Li, Corneil & Mendelsohn (2000), Proposition 2.5.
- ↑ Helden (2007), Corollary 3.78.
- ↑ Bernhart & Kainen (1979).
- ↑ Hakimi & Schmeichel (1979).
- ↑ Skowrońska (1985).
- ↑ Harary & Moser (1966), Corollary 5b.
- ↑ Harary & Moser (1966), Theorem 7.
- ↑ Moon (1966), Theorem 1.
- ↑ Alspach (1967).
- ↑ Häggkvist & Thomassen (1976).
- ↑ Hobbs (1976).
- ↑ Fleischner (1976).
- ↑ Li, Corneil & Mendelsohn (2000), Theorems 2.3 and 2.4.
- ↑ Underground (1978).
References
- Alspach, Brian (1967), "Cycles of each length in regular tournaments", Canadian Mathematical Bulletin 10 (2): 283–286.
- Bernhart, Frank; Kainen, Paul C. (1979), "The book thickness of a graph", Journal of Combinatorial Theory, Series B 27 (3): 320–331, doi:10.1016/0095-8956(79)90021-2.
- Bondy, J. A. (1971), "Pancyclic graphs I", Journal of Combinatorial Theory, Series B 11 (1): 80–84, doi:10.1016/0095-8956(71)90016-5.
- Fleischner, H. (1976), "In the square of graphs, Hamiltonicity and pancyclicity, Hamiltonian connectedness and panconnectedness are equivalent concepts", Monatshefte für Mathematik 82 (2): 125–149, doi:10.1007/BF01305995, MR 0427135.
- Häggkvist, Roland; Thomassen, Carsten (1976), "On pancyclic digraphs", Journal of Combinatorial Theory, Series B 20 (1): 20–40, doi:10.1016/0095-8956(76)90063-0.
- Hakimi, S. L.; Schmeichel, E. F. (1979), "On the number of cycles of length k in a maximal planar graph", Journal of Graph Theory 3: 69–86, doi:10.1002/jgt.3190030108.
- Harary, Frank; Moser, Leo (1966), "The theory of round robin tournaments", American Mathematical Monthly 73 (3): 231–246, doi:10.2307/2315334.
- Helden, Guido (2007), Hamiltonicity of maximal planar graphs and planar triangulations, Dissertation, Rheinisch-Westfälischen Technischen Hochschule Aachen.
- Hobbs, Arthur M. (1976), "The square of a block is vertex pancyclic", Journal of Combinatorial Theory, Series B 20 (1): 1–4, doi:10.1016/0095-8956(76)90061-7, MR 0416980.
- Li, Ming-Chu; Corneil, Derek G.; Mendelsohn, Eric (2000), "Pancyclicity and NP-completeness in planar graphs", Discrete Applied Mathematics 98 (3): 219–225, doi:10.1016/S0166-218X(99)00163-8.
- Malkevitch, Joseph (1971), "On the lengths of cycles in planar graphs", Recent Trends in Graph Theory, Lecture Notes in Mathematics 186, Springer-Verlag, pp. 191–195, doi:10.1007/BFb0059437.
- Moon, J. W. (1966), "On subtournaments of a tournament", Canadian Mathematical Bulletin 9 (3): 297–301, doi:10.4153/CMB-1966-038-7.
- Randerath, Bert; Schiermeyer, Ingo; Tewes, Meike; Volkmann, Lutz (2002), "Vertex pancyclic graphs", Discrete Applied Mathematics 120 (1-3): 219–237, doi:10.1016/S0166-218X(01)00292-X.
- Schmeichel, Edward; Mitchem, John (1982), "Bipartite graphs with cycles of all even lengths", Journal of Graph Theory 6 (4): 429–439, doi:10.1002/jgt.3190060407.
- Skowrońska, Mirosława (1985), "The pancyclicity of Halin graphs and their exterior contractions", in Alspach, Brian R.; Godsil, Christopher D., Cycles in Graphs, Annals of Discrete Mathematics 27, Elsevier Science Publishers B.V., pp. 179–194.
- Underground, Paris (1978), "On graphs with Hamiltonian squares", Discrete Mathematics 21 (3): 323, doi:10.1016/0012-365X(78)90164-4, MR 522906.