P-adically closed field

From Wikipedia, the free encyclopedia

In mathematics, a p-adically closed field is a field that enjoys a closure property that is a close analogue for p-adic fields to what real closure is to the real field. They were introduced by James Ax and Simon B. Kochen in 1965.^[1]

Definition

Let K be the field ℚ of rational numbers and v be its usual p-adic valuation (with $v(p)=1$ ). If F is a (not necessarily algebraic) extension field of K, itself equipped with a valuation w, we say that $(F,w)$ is formally p-adic when the following conditions are satisfied:

w extends v (that is, $w(x)=v(x)$ for all x in K),
the residue field of w coincides with the residue field of v (the residue field being the quotient of the valuation ring 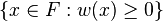$\{x\in F:w(x)\geq 0\}$ by its maximal ideal $\{x\in F:w(x)>0\}$ ),
the smallest positive value of w coincides with the smallest positive value of v (namely 1, since v was assumed to be normalized): in other words, a uniformizer for K remains a uniformizer for F.

(Note that the value group of K may be larger than that of F since it may contain infinitely large elements over the latter.)

The formally p-adic fields can be viewed as an analogue of the formally real fields.

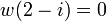For example, the field ℚ(i) of Gaussian rationals, if equipped with the valuation w given by $w(2+i)=1$ (and $w(2-i)=0$ ) is formally 5-adic (the place v=5 of the rationals splits in two places of the Gaussian rationals since 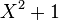$X^{2}+1$ factors over the residue field with 5 elements, and w is one of these places). The field of 5-adic numbers (which contains both the rationals and the Gaussian rationals embedded as per the place w) is also formally 5-adic. On the other hand, the field of Gaussian rationals is not formally 3-adic for any valuation, because the only valuation w on it which extends the 3-adic valuation is given by $w(3)=1$ and its residue field has 9 elements.

When F is formally p-adic but that there does not exist any proper algebraic formally p-adic extension of F, then F is said to be p-adically closed. For example, the field of p-adic numbers is p-adically closed, and so is the algebraic closure of the rationals inside it (the field of p-adic algebraic numbers).

If F is p-adically closed, then:^[2]

there is a unique valuation w on F which makes F p-adically closed (so it is legitimate to say that F, rather than the pair $(F,w)$ , is p-adically closed),
F is Henselian with respect to this place (that is, its valuation ring is so),
the valuation ring of F is exactly the image of the Kochen operator (see below),
the value group of F is an extension by ℤ (the value group of K) of a divisible group, with the lexicographical order.

The first statement is an analogue of the fact that the order of a real-closed field is uniquely determined by the algebraic structure.

The definitions given above can be copied to a more general context: if K is a field equipped with a valuation v such that

the residue field of K is finite (call q its cardinal and p its characteristic),
the value group of v admits a smallest positive element (call it 1, and say π is a uniformizer, i.e. $v(\pi )=1$ ),
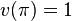K has finite absolute ramification, i.e., 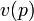$v(p)$ is finite (that is, a finite multiple of $v(\pi )=1$ ),

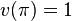(these hypotheses are satisfied for the field of rationals, with q=π=p the prime number having valuation 1) then we can speak of formally v-adic fields (or ${\mathfrak {p}}$ -adic if ${\mathfrak {p}}$ is the ideal corresponding to v) and v-adically complete fields.

The Kochen operator

If K is a field equipped with a valuation v satisfying the hypothesis and with the notations introduced in the previous paragraph, define the Kochen operator by:

$\gamma (z)={\frac {1}{\pi }}\,{\frac {z^{q}-z}{(z^{q}-z)^{2}-1}}$

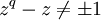(when $z^{q}-z\neq \pm 1$ ). It is easy to check that 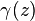$\gamma (z)$ always has non-negative valuation. The Kochen operator can be thought of as a p-adic (or v-adic) analogue of the square function in the real case.

An extension field F of K is formally v-adic if and only if ${\frac {1}{\pi }}$ does not belong to the subring generated over the value ring of K by the image of the Kochen operator on F. This is an analogue of the statement (or definition) that a field is formally real when $-1$ is not a sum of squares.

First-order theory

The first-order theory of p-adically closed fields (here we are restricting ourselves to the p-adic case, i.e., K is the field of rationals and v is the p-adic valuation) is complete and model complete, and if we slightly enrich the language it admits quantifier elimination. Thus, one can define p-adically closed fields as those whose first-order theory is elementarily equivalent to that of ${\mathbb {Q}}_{p}$ .

References

Ax, James; Kochen, Simon (1965). "Diophantine problems over local fields. II. A complete set of axioms for 푝-adic number theory". Amer. J. Math. (The Johns Hopkins University Press) 87 (3): 631–648. doi:10.2307/2373066. JSTOR 2373066.

Kochen, Simon (1969). "Integer valued rational functions over the 푝-adic numbers: A 푝-adic analogue of the theory of real fields". Number Theory (Proc. Sympos. Pure Math., Vol. XII, Houston, Tex., 1967). American Mathematical Society. pp. 57–73.

Kuhlmann, F.-V. "푝-adically closed field". Springer Online Reference Works: Encyclopaedia of Mathematics. Springer-Verlag. Retrieved 2009-02-03.

Jarden, Moshe; Roquette, Peter (1980). "The Nullstellensatz over 픭-adically closed fields". J. Math. Soc. Japan 32 (3): 425–460. doi:10.2969/jmsj/03230425.

Notes

↑ Ax & Kochen (1965)
↑ Jarden & Roquette (1980), lemma 4.1

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.