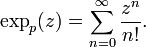P-adic exponential function

From Wikipedia, the free encyclopedia

In mathematics, particularly p-adic analysis, the p-adic exponential function is a p-adic analogue of the usual exponential function on the complex numbers. As in the complex case, it has an inverse function named the p-adic logarithm.

Definition

The usual exponential function on C is defined by the infinite series

$\exp(z)=\sum _{{n=0}}^{\infty }{\frac {z^{n}}{n!}}.$

Entirely analogously, one defines the exponential function on C_p, the completion of the algebraic closure of Q_p, by

$\exp _{p}(z)=\sum _{{n=0}}^{\infty }{\frac {z^{n}}{n!}}.$

However, unlike exp which converges on all of C, exp_p only converges on the disc

$|z|_{p}<p^{{-1/(p-1)}}.$

This is because p-adic series converge if and only if the summands tend to zero, and since the n! in the denominator of each summand tends to make them very large p-adically, rather a small value of z is needed in the numerator.

p-adic logarithm function

The power series

$\log(1+x)=\sum _{{n=1}}^{\infty }{\frac {(-1)^{{n+1}}x^{n}}{n}},$

converges for x in C_p satisfying |x|_p < 1 and so defines the p-adic logarithm function log_p(z) for |z − 1|_p < 1 satisfying the usual property log_p(zw) = log_pz + log_pw. The function log_p can be extended to all of C ×
p (the set of nonzero elements of C_p) by imposing that it continue to satisfy this last property and setting log_p(p) = 0. Specifically, every element w of C ×
p can be written as w = p^r·ζ·z with r a rational number, ζ a root of unity, and |z − 1|_p < 1,^[1] in which case log_p(w) = log_p(z).^[2] This function on C ×
p is sometimes called the Iwasawa logarithm to emphasize the choice of log_p(p) = 0. In fact, there is an extension of the logarithm from |z − 1|_p < 1 to all of C ×
p for each choice of log_p(p) in C_p.^[3]

Properties

If z and w are both in the radius of convergence for exp_p, then their sum is too and we have the usual addition formula: exp_p(z + w) = exp_p(z)exp_p(w).

Similarly if z and w are nonzero elements of C_p then log_p(zw) = log_pz + log_pw.

And for suitable z, so that everything is defined, we have exp_p(log_p(z)) = z and log_p(exp_p(z)) = z.

The roots of the Iwasawa logarithm log_p(z) are exactly the elements of C_p of the form p^r·ζ where r is a rational number and ζ is a root of unity.^[4]

Note that there is no analogue in C_p of Euler's identity, e^2πi = 1. This is a corollary of Strassmann's theorem.

Another major difference to the situation in C is that the domain of convergence of exp_p is much smaller than that of log_p. A modified exponential function — the Artin–Hasse exponential — can be used instead which converges on |z|_p < 1.

Notes

↑ Cohen 2007, Proposition 4.4.44
↑ In factoring w as above, there is a choice of a root involved in writing p^r since r is rational; however, different choices differ only by multiplication by a root of unity, which gets absorbed into the factor ζ.
↑ Cohen 2007, §4.4.11
↑ Cohen 2007, Proposition 4.4.45

References

Chapter 12 of Cassels, J. W. S. (1986). Local fields. London Mathematical Society Student Texts. Cambridge University Press. ISBN 0-521-31525-5.
Cohen, Henri (2007), Number theory, Volume I: Tools and Diophantine equations, Graduate Texts in Mathematics 239, New York: Springer, doi:10.1007/978-0-387-49923-9, ISBN 978-0-387-49922-2, MR 2312337

External links

p-adic exponential and p-adic logarithm, PlanetMath.org.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.