Pépin's test

From Wikipedia, the free encyclopedia

In mathematics, Pépin's test is a primality test, which can be used to determine whether a Fermat number is prime. It is a variant of Proth's test. The test is named for a French mathematician, Théophile Pépin.

Description of the test

Let $F_{n}=2^{{2^{n}}}+1$ be the nth Fermat number. Pépin's test states that for n > 0,

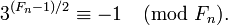
$F_{n}$ is prime if and only if $3^{{(F_{n}-1)/2}}\equiv -1{\pmod {F_{n}}}.$

The expression $3^{{(F_{n}-1)/2}}$ can be evaluated modulo $F_{n}$ by repeated squaring. This makes the test a fast polynomial-time algorithm. However, Fermat numbers grow so rapidly that only a handful of Fermat numbers can be tested in a reasonable amount of time and space.

Other bases may be used in place of 3, for example 5, 6, 7, or 10 (sequence A129802 in OEIS).

Proof of correctness

Sufficiency: assume that the congruence

$3^{{(F_{n}-1)/2}}\equiv -1{\pmod {F_{n}}}$

holds. Then $3^{{F_{n}-1}}\equiv 1{\pmod {F_{n}}}$ , thus the multiplicative order of 3 modulo $F_{n}$ divides $F_{n}-1=2^{{2^{n}}}$ , which is a power of two. On the other hand, the order does not divide $(F_{n}-1)/2$ , and therefore it must be equal to $F_{n}-1$ . In particular, there are at least $F_{n}-1$ numbers below $F_{n}$ coprime to $F_{n}$ , and this can happen only if $F_{n}$ is prime.

Necessity: assume that $F_{n}$ is prime. By Euler's criterion,

$3^{{(F_{n}-1)/2}}\equiv \left({\frac 3{F_{n}}}\right){\pmod {F_{n}}}$ ,

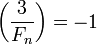where $\left({\frac 3{F_{n}}}\right)$ is the Legendre symbol. By repeated squaring, we find that $2^{{2^{n}}}\equiv 1{\pmod 3}$ , thus $F_{n}\equiv 2{\pmod 3}$ , and $\left({\frac {F_{n}}3}\right)=-1$ . As $F_{n}\equiv 1{\pmod 4}$ , we conclude $\left({\frac 3{F_{n}}}\right)=-1$ from the law of quadratic reciprocity.

Historical Pépin tests

Because of the sparsity of the Fermat numbers, the Pépin test has only been run seven times (on Fermat numbers whose primality statuses were not already known).^[1]^[2] Mayer, Papadopoulos and Crandall speculate that in fact, because of the size of the still undetermined Fermat numbers, it will take decades before technology allows any more Pépin tests to be run.^[3] As of 2012 the smallest untested Fermat number with no known prime factor is $F_{{33}}$ which has 2,585,827,973 digits.

Year	Provers	Fermat number	Pépin test result	Factor found later?
1905	Morehead & Western	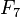$F_{{7}}$	composite	Yes (1970)
1909	Morehead & Western	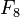$F_{{8}}$	composite	Yes (1980)
1960	Paxson	$F_{{13}}$	composite	Yes (1974)
1961	Selfridge & Hurwitz	$F_{{14}}$	composite	Yes (2010)
1987	Buell & Young	$F_{{20}}$	composite	No
1993	Crandall, Doenias, Norrie & Young	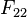$F_{{22}}$	composite	Yes (2010)
1999	Mayer, Papadopoulos & Crandall	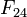$F_{{24}}$	composite	No

Notes

↑ Conjecture 4. Fermat primes are finite - Pepin tests story, according to Leonid Durman
↑ Wilfrid Keller: Fermat factoring status
↑ Richard E. Crandall, Ernst W. Mayer & Jason S. Papadopoulos, The twenty-fourth Fermat number is composite (2003)

References

P. Pépin, Sur la formule 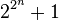$2^{{2^{n}}}+1$ , Comptes Rendus Acad. Sci. Paris 85 (1877), pp. 329–333.

External links

The Prime Glossary: Pepin's test

v t e Number-theoretic algorithms

Primality tests	AKS test APR test Baillie–PSW ECPP test Elliptic curve Pocklington Fermat Lucas Lucas–Lehmer Lucas–Lehmer–Riesel Proth's theorem Pépin's Quadratic Frobenius test Solovay–Strassen Miller–Rabin Trial division

Prime-generating	Sieve of Atkin Sieve of Eratosthenes Sieve of Sundaram Wheel factorization

Integer factorization	Continued fraction (CFRAC) Dixon's Lenstra elliptic curve (ECM) Euler's Pollard's rho p − 1 p + 1 Quadratic sieve (QS) General number field sieve (GNFS) Special number field sieve (SNFS) Rational sieve Fermat's Shanks' square forms Trial division Shor's

Multiplication	Ancient Egyptian Karatsuba Toom–Cook Schönhage–Strassen Fürer's

Discrete logarithm	Baby-step giant-step Pollard rho Pollard kangaroo Pohlig–Hellman Index calculus Function field sieve

Greatest common divisor	Binary Euclidean Extended Euclidean Lehmer's

Modular square root	Cipolla Pocklington's Tonelli–Shanks

Other algorithms	Chakravala Cornacchia Integer relation Integer square root Modular exponentiation Schoof's

Italics indicate that algorithm is for numbers of special forms Smallcaps indicate a deterministic algorithm

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.