Ovoid (projective geometry)

From Wikipedia, the free encyclopedia

In the projective space PG(3,q), with q a prime power greater than 2, an ovoid is a set of 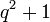q^{2}+1 points, no three of which are collinear (the maximum size of such a set).[1] When q=2 the largest set of non-collinear points has size eight and is the complement of a plane.[2]

An important example of an ovoid in any finite projective three-dimensional space are the 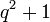q^{2}+1 points of an elliptic quadric (all of which are projectively equivalent).

When q is odd or 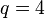q=4, no ovoids exist other than the elliptic quadrics.[3]

When 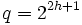q=2^{{2h+1}} another type of ovoid can be constructed : the Tits ovoid, also known as the Suzuki ovoid. It is conjectured that no other ovoids exist in PG(3,q).

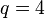Through every point P on the ovoid, there are exactly q+1 tangents, and it can be proven that these lines are exactly the lines through P in one specific plane through P. This means that through every point P in the ovoid, there is a unique plane intersecting the ovoid in exactly one point.[4] Also, if q is odd or q=4 every plane which is not a tangent plane meets the ovoid in a conic.[5]

See also

Notes

  1. ↑ more properly the term should be ovaloid and ovoid has a different definition which extends to projective spaces of higher dimension. However, in dimension 3 the two concepts are equivalent and the ovoid terminology is almost universally used, except most notably, in Hirschfeld.
  2. ↑ Hirschfeld 1985, pg.33, Theorem 16.1.3
  3. ↑ Barlotti 1955 and Panella 1955
  4. ↑ Hirschfeld 1985, pg. 34, Lemma 16.1.6
  5. ↑ Hirschfeld 1985, pg.35, Corollary

References

  • Barlotti, A. (1955), "Un' estensione del teorema di Segre-Kustaanheimo", Boll. Un. Mat. Ital. 10: 96–98 
  • Hirschfeld, J.W.P. (1985), Finite Projective Spaces of Three Dimensions, New York: Oxford University Press, ISBN 0-19-853536-8 
  • Panella, G. (1955), "Caratterizzazione delle quadriche di uno spazio (tridimensionale) lineare sopra un corpo finito", Boll. Un. Mat. Ital. 10: 507–513 


This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.