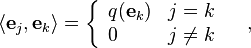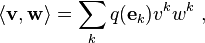Orthogonal basis

From Wikipedia, the free encyclopedia

In mathematics, particularly linear algebra, an orthogonal basis for an inner product space $V$ is a basis for $V$ whose vectors are mutually orthogonal. If the vectors of an orthogonal basis are normalized, the resulting basis is an orthonormal basis.

In functional analysis, an orthogonal basis is any basis obtained from an orthonormal basis (or Hilbert basis) using multiplication by nonzero scalars.

Any orthogonal basis can be used to define a system of orthogonal coordinates $V$ . Orthogonal (not necessarily orthonormal) bases are important due to their appearance from curvilinear orthogonal coordinates in Euclidean spaces, as well as in Riemannian and pseudo-Riemannian manifolds.

The concept of an orthogonal (but not of an orthonormal) basis is applicable to a vector space $V$ (over any field) equipped with a symmetric bilinear form $⟨ \cdot,\cdot ⟩$ , where orthogonality of two vectors $v$ and $w$ means $⟨ v, w ⟩ = 0$ . For an orthogonal basis ${e k}$ :

$\langle {\mathbf {e}}_{j},{\mathbf {e}}_{k}\rangle =\left\{{\begin{array}{ll}q({\mathbf {e}}_{k})&j=k\\0&j\neq k\end{array}}\right.\quad ,$

where $q$ is a quadratic form associated with $⟨ \cdot,\cdot ⟩$ : $q (v) = ⟨ v, v ⟩$ (in an inner product space $q (v) = | v | 2$ ). Hence,

$\langle {\mathbf {v}},{\mathbf {w}}\rangle =\sum \limits _{{k}}q({\mathbf {e}}_{k})v^{k}w^{k}\ ,$

where $v k$ and $w k$ are components of $v$ and $w$ in ${e k}$ .

References

Lang, Serge (2004), Algebra, Graduate Texts in Mathematics 211 (Corrected fourth printing, revised third ed.), New York: Springer-Verlag, pp. 572–585, ISBN 978-0-387-95385-4
Milnor, J.; Husemoller, D. (1973). Symmetric Bilinear Forms. Ergebnisse der Mathematik und ihrer Grenzgebiete 73. Springer-Verlag. p. 6. ISBN 3-540-06009-X. Zbl 0292.10016.

External links

Weisstein, Eric W., "Orthogonal Basis", MathWorld.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.