Orlicz–Pettis theorem

From Wikipedia, the free encyclopedia

In functional analysis, the Orlicz–Pettis theorem is a theorem about convergence in Banach spaces. It is named for Władysław Orlicz and Billy James Pettis.[1][2] The result was originally proven by Orlicz for weakly sequentially complete normed spaces.[3]

Orlicz–Pettis Theorem for Banach spaces

Let X be a Banach space and let 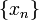\left\{{{x}_{{n}}}\right\} be any sequence in X. If the series \sum {{{x}_{{n}}}} is weakly subseries convergent, then the series is actually subseries convergent in the norm topology of X.

References

  1. ↑ Orlicz, W. (1929), "Beiträge zur Theorie der Orthogonalentwicklungen. I, II", Studia (in German) 1: 1–39, 241–255, Zbl 55.0164.02 .
  2. ↑ Pettis, B. J. (1938), "On integration in vector spaces", Transactions of the American Mathematical Society 44 (2): 277–304, doi:10.2307/1989973, MR 1501970 .
  3. ↑ Diestel, J.; Uhl, J. J., Jr. (1977), Vector Measures, Mathematical Surveys 15, Providence, R.I.: American Mathematical Society, p. 34, MR 0453964 .


This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.