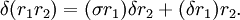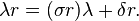Ore extension

From Wikipedia, the free encyclopedia

In mathematics, especially in the area of algebra known as ring theory, an Ore extension, named after Øystein Ore, is a special type of a ring extension whose properties are relatively well understood. Ore extensions appear in several natural contexts, including skew and differential polynomial rings, group algebras of polycyclic groups, universal enveloping algebras of solvable Lie algebras, and coordinate rings of quantum groups.

Definition

Suppose that R is a ring, σ:R → R is an injective ring homomorphism, and δ:R → R is a σ-derivation of R, which means that δ is a homomorphism of abelian groups satisfying

$\delta (r_{1}r_{2})=(\sigma r_{1})\delta r_{2}+(\delta r_{1})r_{2}.$

Then the Ore extension R[λ;σ,δ] is the ring obtained by giving the ring of polynomials R[λ] a new multiplication, subject to the identity

$\lambda r=(\sigma r)\lambda +\delta r.$

If δ = 0 (i.e., is the zero map) then the Ore extension is denoted R[λ; σ] and is called a skew polynomial ring. If σ = 1 (i.e., the identity map) then the Ore extension is denoted R[λ,δ] and is called a differential polynomial ring.

Examples

The Weyl algebras are Ore extensions, with R any a commutative polynomial ring, σ the identity ring endomorphism, and δ the polynomial derivative.

Properties

An Ore extension of a domain is a domain.
If σ is an automorphism and R is a left Noetherian ring then the Ore extension R[λ;σ,δ] is also left Noetherian.

References

Goodearl, K. R.; Warfield, R. B., Jr. (2004), An Introduction to Noncommutative Noetherian Rings, Second Edition, London Mathematical Society Student Texts 61, Cambridge: Cambridge University Press, ISBN 0-521-83687-5; 0-521-54537-4 Check |isbn= value (help), MR 2080008
McConnell, J. C.; Robson, J. C. (2001), Noncommutative Noetherian rings, Graduate Studies in Mathematics 30, Providence, R.I.: American Mathematical Society, ISBN 978-0-8218-2169-5, MR 1811901
Rowen, Louis H. (1988), Ring theory, vol. I, II, Pure and Applied Mathematics, 127, 128, Boston, MA: Academic Press, ISBN 978-0-12-599841-3, ISBN 0-12-599841-4 Check |isbn= value (help), MR 940245

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.