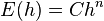Order of accuracy

From Wikipedia, the free encyclopedia

In numerical analysis, order of accuracy quantifies the rate of convergence of a numerical approximation of a differential equation to the exact solution. A numerical solution to a differential equation is said to be $n$ th-order accurate if the error, $E$ , is proportional to the step-size $h$ to the $n$ th power;^[1]

$E(h)=Ch^{n}$

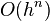The size of the error of a first-order accurate approximation is directly proportional to $h$ . In big O notation, an $n$ th-order accurate numerical method is notated as $O(h^{n})$ . Partial differential equations which vary over both time and space are said to be accurate to order $n$ in time and to order $m$ in space.^[2]

The order of accuracy of several numerical methods are given below.

Method	Order of accuracy
Forward difference, backward difference	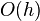$O(h)$
Central difference	$O(h^{2})$
Fourth-order Runge–Kutta method	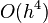$O(h^{4})$

References

↑ LeVeque, Randall J (2006). Finite Difference Methods for Differential Equations. University of Washington. pp. 3–5.
↑ Strikwerda, John C (2004). Finite Difference Schemes and Partial Differential Equations (2 ed.). pp. 62–66. ISBN 978-0-898716-39-9.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.