Omnitruncated 7-simplex honeycomb

From Wikipedia, the free encyclopedia
Omnitruncated 7-simplex honeycomb
(No image)
TypeUniform honeycomb
FamilyOmnitruncated simplectic honeycomb
Schläfli symbol{3[8]}
Coxeter–Dynkin diagrams
6-face typest0123456{3,3,3,3,3,3}
Vertex figure
Irr. 7-simplex
Symmetry{{\tilde {A}}}_{8}×16, [8[3[8]]]
Propertiesvertex-transitive

In seven-dimensional Euclidean geometry, the omnitruncated 7-simplex honeycomb is a space-filling tessellation (or honeycomb). It is composed entirely of omnitruncated 7-simplex facets.

The facets of all omnitruncated simplectic honeycombs are called permutahedra and can be positioned in n+1 space with integral coordinates, permutations of the whole numbers (0,1,..,n).

A7* lattice

The A*
7 lattice (also called A8
7) is the union of eight A7 lattices, and has the vertex arrangement to the dual honeycomb of the omnitruncated 7-simplex honeycomb, and therefore the Voronoi cell of this lattice is an omnitruncated 7-simplex.

+ + + + + + + = dual of .

Related polytopes and honeycombs

This honeycomb is one of 29 unique uniform honeycombs[1] constructed by the {{\tilde {A}}}_{7} Coxeter group, grouped by their extended symmetry of rings within the regular octagon diagram:

Octagon
symmetry		 Extended
symmetry		 Extended
diagram		 Extended
order		 Honeycombs
a1 [3[8]] ×1

d2 <[3[8]]> ×2

1

p2 [[3[8]]] ×2

2

d4 <2[3[8]]> ×4

p4 [2[3[8]]] ×4

d8 [4[3[8]]] ×8
r16 [8[3[8]]] ×16 3

See also

Regular and uniform honeycombs in 7-space:

Notes

  1. ↑ Weisstein, Eric W., "Necklace", MathWorld., A000029 30-1 cases, skipping one with zero marks

References

  • Norman Johnson Uniform Polytopes, Manuscript (1991)
  • Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
    • (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10] (1.9 Uniform space-fillings)
    • (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
Fundamental convex regular and uniform honeycombs in dimensions 2–11
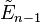Family {{\tilde {A}}}_{{n-1}} {{\tilde {C}}}_{{n-1}} {{\tilde {B}}}_{{n-1}} {{\tilde {D}}}_{{n-1}} {{\tilde {G}}}_{2} / {{\tilde {F}}}_{4} / {{\tilde {E}}}_{{n-1}}
Uniform tiling {3[3]} δ3 hδ3 qδ3 Hexagonal
Uniform convex honeycomb {3[4]} δ4 hδ4 qδ4
Uniform 5-honeycomb {3[5]} δ5 hδ5 qδ5 24-cell honeycomb
Uniform 6-honeycomb {3[6]} δ6 hδ6 qδ6
Uniform 7-honeycomb {3[7]} δ7 hδ7 qδ7 222
Uniform 8-honeycomb {3[8]} δ8 hδ8 qδ8 133 • 331
Uniform 9-honeycomb {3[9]} δ9 hδ9 qδ9 152 • 251 • 521
Uniform n-honeycomb {3[n]} δn hδn qδn 1k2 • 2k1 • k21
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.