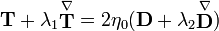Oldroyd-B model

From Wikipedia, the free encyclopedia

The Oldroyd-B model is a constitutive model used to describe the flow of viscoelastic fluids. This model can be regarded as an extension of the Upper Convected Maxwell model and is equivalent to a fluid filled with elastic bead and spring dumbbells. The model is named after its creator James G. Oldroyd.

The model can be written as:

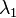${\mathbf {T}}+\lambda _{1}{\stackrel {\nabla }{{\mathbf {T}}}}=2\eta _{0}({\mathbf {D}}+\lambda _{2}{\stackrel {\nabla }{{\mathbf {D}}}})$

where:

${\mathbf {T}}$ is the stress tensor;
$\lambda _{1}$ is the relaxation time;
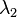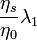$\lambda _{2}$ is the retardation time = ${\frac {\eta _{s}}{\eta _{0}}}\lambda _{1}$ ;
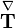${\stackrel {\nabla }{{\mathbf {T}}}}$ is the Upper convected time derivative of stress tensor:

${\stackrel {\nabla }{{\mathbf {T}}}}={\frac {\partial }{\partial t}}{\mathbf {T}}+{\mathbf {v}}\cdot \nabla {\mathbf {T}}-((\nabla {\mathbf {v}})^{T}\cdot {\mathbf {T}}+{\mathbf {T}}\cdot (\nabla {\mathbf {v}}))$ ;

${\mathbf {v}}$ is the fluid velocity;
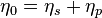$\eta _{0}$ is the total viscosity composed of solvent and polymer components, $\eta _{0}=\eta _{s}+\eta _{p}$ ;
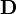${\mathbf {D}}$ is the deformation rate tensor or rate of strain tensor, ${\mathbf {D}}={\frac {1}{2}}\left[{\boldsymbol \nabla }{\mathbf {v}}+({\boldsymbol \nabla }{\mathbf {v}})^{T}\right]$ .

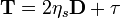The model can also be written split into polymeric (viscoelastic) part separately from the solvent part: ${\mathbf {T}}=2\eta _{s}{\mathbf {D}}+{\mathbf {\tau }}$ .

where

${\mathbf {\tau }}+\lambda _{1}{\stackrel {\nabla }{{\mathbf {\tau }}}}=2\eta _{p}{\mathbf {D}}$

Whilst the model gives good approximations of viscoelastic fluids in shear flow, it has an unphysical singularity in extensional flow, where the dumbbells are infinitely stretched; If the solvent viscosity is zero then the Oldroyd-B becomes the Upper Convected Maxwell model.

References

Oldroyd, James (Feb 1950). "On the Formulation of Rheological Equations of State". Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences 200 (1063): 523–541. Cite uses deprecated parameters (help)

Owens, R. G.,Phillips, T. N. (2002). Computational Rheology. Imperial College Press. ISBN 978-1-86094-186-3.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.