Octahemioctahedron
| Octahemioctahedron | |
|---|---|
 | |
| Type | Uniform star polyhedron |
| Elements | F = 12, E = 24 V = 12 (χ = 0) |
| Faces by sides | 8{3}+4{6} |
| Wythoff symbol(s) | 3/2 3 | 3 |
| Symmetry group | Oh, [4,3], *432 Td, [3,3], *332 |
| Index references | U03, C37, W68 |
| Bowers acronym | Oho |
 3.6.3/2.6 (Vertex figure) |
 Octahemioctacron (dual polyhedron) |
In geometry, the octahemioctahedron is a nonconvex uniform polyhedron, indexed as U3. Its vertex figure is a crossed quadrilateral.
It is one of nine hemipolyhedra with 4 hexagonal faces passing through the model center.
Related polyhedra
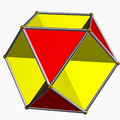
It shares the vertex arrangement and edge arrangement with the cuboctahedron (having the triangular faces in common), and with the cubohemioctahedron (having the hexagonal faces in common).
By Wythoff construction it has tetrahedral symmetry (Td), like the rhombitetratetrahedron construction for the cuboctahedron, with alternate triangles with inverted orientations. Without alternating triangles, it has octahedral symmetry (Oh).
| Cuboctahedron | Cubohemioctahedron | Octahemioctahedron | ||
|---|---|---|---|---|
| Octahedral symmetry | Tetrahedral symmetry | Octahedral symmetry | Tetrahedral symmetry | |
 |
 |
 |
 |
 |
| 2 | 3 4 | 3 3 | 2 | 4/3 4 | 3 (double cover) |
3/2 3 | 3 | |
| |
|
|
| |
Orientability
It is the only hemipolyhedron that is orientable, and the only uniform polyhedron with an Euler characteristic of zero (a topological torus).
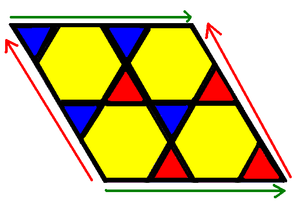 The topological net of faces can be arranged as a rhombus divided into 8 triangles and 4 hexagons. All vertex angle defects are zero. |
 The net represents a region of the trihexagonal tiling plane, with Wythoff symbol 3 3 | 3 and Coxeter-Dynkin diagram |