Objective stress rates
In continuum mechanics, objective stress rates are time derivatives of stress that do not depend on the frame of reference.[1] Many constitutive equations are designed in the form of a relation between a stress-rate and a strain-rate (or the rate of deformation tensor). The mechanical response of a material should not depend on the frame of reference. In other words, material constitutive equations should be frame indifferent (objective). If the stress and strain measures are material quantities then objectivity is automatically satisfied. However, if the quantities are spatial, then the objectivity of the stress-rate is not guaranteed even if the strain-rate is objective.
There are numerous objective stress rates in continuum mechanics - all of which can be shown to be special forms of Lie derivatives. Some of the widely used objective stress rates are:
- the Truesdell rate of the Cauchy stress tensor,
- the Green-Naghdi rate of the Cauchy stress, and
- the Jaumann rate of the Cauchy stress.
The adjacent figure shows the performance of various objective rates in a pure shear test where the material model is hypoelastic with constant elastic moduli. The ratio of the shear stress to the displacement is plotted as a function of time. The same moduli are used with the three objective stress rates. Clearly there are spurious oscillations observed for the Jaumann stress rate. This is not because one rate is better than another but because it is a misuse of material models to use the same constants with different objective rates. For this reason, a recent trend has been to avoid objective stress rates altogether where possible.
Non-objectivity of the time derivative of Cauchy stress
Under rigid body rotations (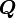 ), the Cauchy stress tensor
), the Cauchy stress tensor 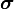 transforms as
transforms as
Since 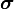 is a spatial quantity and the transformation follows the rules of tensor transformations,
is a spatial quantity and the transformation follows the rules of tensor transformations, 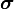 is objective. However,
is objective. However,
Therefore the stress rate is not objective unless the rate of rotation is zero, i.e. 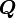 is constant.
is constant.
Truesdell stress rate of the Cauchy stress
The relation between the Cauchy stress and the 2nd P-K stress is called
the Piola transformation. This transformation can be
written in terms of the pull-back of 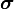 or the push-forward of
or the push-forward of 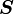 as
as
The Truesdell rate of the Cauchy stress is the Piola transformation of the material time derivative of the 2nd P-K stress. We thus define
Expanded out, this means that
where the Kirchhoff stress  and the Lie derivative of
the Kirchhoff stress is
and the Lie derivative of
the Kirchhoff stress is
This expression can be simplified to the well known expression for the Truesdell rate of the Cauchy stress
|
Truesdell rate of the Cauchy stress
| |||
It can be shown that the Truesdell rate is objective.
Truesdell rate of the Kirchhoff stress
The Truesdell rate of the Kirchhoff stress can be obtained by noting that
and defining
Expanded out, this means that
Therefore, the Lie derivative of  is the same as the Truesdell rate of the Kirchhoff stress.
is the same as the Truesdell rate of the Kirchhoff stress.
FFollowing the same process as for the Cauchy stress above, we can show that
|
Truesdell rate of the Kirchhoff stress |
Green-Naghdi rate of the Cauchy stress
This is a special form of the Lie derivative (or the Truesdell rate of the Cauchy stress). Recall that the Truesdell rate of the Cauchy stress is given by
From the polar decomposition theorem we have
where  is the orthogonal rotation tensor (
is the orthogonal rotation tensor ( )
and
)
and  is the symmetric, positive definite, right stretch.
is the symmetric, positive definite, right stretch.
If we assume that 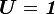 we get
we get  . Also since there is no
stretch
. Also since there is no
stretch  and we have
and we have  . Note that this doesn't mean
that there is not stretch in the actual body - this simplification is just
for the purposes of defining an objective stress rate. Therefore
. Note that this doesn't mean
that there is not stretch in the actual body - this simplification is just
for the purposes of defining an objective stress rate. Therefore
We can show that this expression can be simplified to the commonly used form of the Green-Naghdi rate
|
Green-Naghdi rate of the Cauchy stress where
| |||
The Green-Naghdi rate of the Kirchhoff stress also has the form since the stretch is not taken into consideration, i.e.,
Jaumann rate of the Cauchy stress
The Jaumann rate of the Cauchy stress is a further specialization of the Lie derivative (Truesdell rate). This rate has the form
|
Jaumann rate of the Cauchy stress where |
The Jaumann rate is used widely in computations primarily for two reasons
- it is relatively easy to implement.
- it leads to symmetric tangent moduli.
Recall that the spin tensor  (the skew part of the velocity gradient)
can be expressed as
(the skew part of the velocity gradient)
can be expressed as
Thus for pure rigid body motion
Alternatively, we can consider the case of proportional loading when the principal directions of strain remain constant. An example of this situation is the axial loading of a cylindrical bar. In that situation, since
we have
Also,
![{\boldsymbol {U}}^{{-1}}=\left[{\begin{array}{ccc}1/\lambda _{{X}}\\&1/\lambda _{{Y}}\\&&1/\lambda _{{Z}}\end{array}}\right]](/2014-wikipedia_en_all_02_2014/I/media/3/a/a/4/3aa410dbca2dfa72eb0c32e626ded107.png) of the Cauchy stress
of the Cauchy stress
Therefore,
This once again gives
In general, if we approximate
the Green-Naghdi rate becomes the Jaumann rate of the Cauchy stress
Other objective stress rates
There can be an infinite variety of objective stress rates. One of these is the Oldroyd stress rate
In simpler form, the Oldroyd rate is given by
If the current configuration is assumed to be the reference configuration then
the pull back and push forward operations can be conducted using 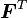 and
and
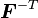 respectively. The Lie derivative of the Cauchy stress is then
called the convective stress rate
respectively. The Lie derivative of the Cauchy stress is then
called the convective stress rate
In simpler form, the convective rate is given by
See also
- Cauchy stress tensor
- Stress measures
- Objectivity (frame invariance)
- Principle of material objectivity
- Hypoelastic material
Notes
- ↑ Gurtin et al. (2010). p. 151,242.
References
- Gurtin, Morton E.; Fried, Eliot; Anand, Lallit (2010), The mechanics and thermodynamics of continua, Cambridge University Press
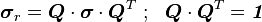

![{\boldsymbol {S}}=J~\phi ^{{*}}[{\boldsymbol {\sigma }}]~;~~{\boldsymbol {\sigma }}=J^{{-1}}~\phi _{{*}}[{\boldsymbol {S}}]](/2014-wikipedia_en_all_02_2014/I/media/1/0/5/5/1055b001bd7b9936b45f83a47405532a.png)
![{\overset {\circ }{{\boldsymbol {\sigma }}}}=J^{{-1}}~\phi _{{*}}[{\dot {{\boldsymbol {S}}}}]](/2014-wikipedia_en_all_02_2014/I/media/4/0/b/c/40bcdabf6f6b90be1aae4db6fd88304b.png)
![{\overset {\circ }{{\boldsymbol {\sigma }}}}=J^{{-1}}~{\boldsymbol {F}}\cdot {\dot {{\boldsymbol {S}}}}\cdot {\boldsymbol {F}}^{T}=J^{{-1}}~{\boldsymbol {F}}\cdot \left[{\cfrac {d}{dt}}\left(J~{\boldsymbol {F}}^{{-1}}\cdot {\boldsymbol {\sigma }}\cdot {\boldsymbol {F}}^{{-T}}\right)\right]\cdot {\boldsymbol {F}}^{T}=J^{{-1}}~{\mathcal {L}}_{\varphi }[{\boldsymbol {\tau }}]](/2014-wikipedia_en_all_02_2014/I/media/4/a/b/4/4ab4c3aaff1e2c2472d5074f97e0227d.png)
![{\mathcal {L}}_{\varphi }[{\boldsymbol {\tau }}]={\boldsymbol {F}}\cdot \left[{\cfrac {d}{dt}}\left({\boldsymbol {F}}^{{-1}}\cdot {\boldsymbol {\tau }}\cdot {\boldsymbol {F}}^{{-T}}\right)\right]\cdot {\boldsymbol {F}}^{T}~.](/2014-wikipedia_en_all_02_2014/I/media/c/8/d/6/c8d676879fc682b57369b7a5e17180f5.png)

![{\overset {\circ }{{\boldsymbol {\sigma }}}}=J^{{-1}}~{\boldsymbol {F}}\cdot \left[{\cfrac {d}{dt}}\left(J~{\boldsymbol {F}}^{{-1}}\cdot {\boldsymbol {\sigma }}\cdot {\boldsymbol {F}}^{{-T}}\right)\right]\cdot {\boldsymbol {F}}^{T}~.](/2014-wikipedia_en_all_02_2014/I/media/3/6/1/3/3613a52388019f7f1663ff8a8a56eaad.png)

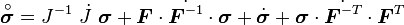
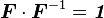
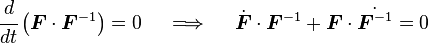
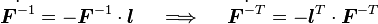
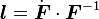 .
.
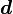 is the rate of deformation tensor.
is the rate of deformation tensor.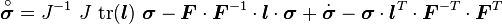
![{\boldsymbol {S}}=\phi ^{{*}}[{\boldsymbol {\tau }}]~;~~{\boldsymbol {\tau }}=\phi _{{*}}[{\boldsymbol {S}}]](/2014-wikipedia_en_all_02_2014/I/media/a/5/9/b/a59b2ec19da77cee36af2170bb59ff43.png)
![{\overset {\circ }{{\boldsymbol {\tau }}}}=\phi _{{*}}[{\dot {{\boldsymbol {S}}}}]](/2014-wikipedia_en_all_02_2014/I/media/4/2/c/8/42c867f6a7db088675ecf9a0cb27a2eb.png)
![{\overset {\circ }{{\boldsymbol {\tau }}}}={\boldsymbol {F}}\cdot {\dot {{\boldsymbol {S}}}}\cdot {\boldsymbol {F}}^{T}={\boldsymbol {F}}\cdot \left[{\cfrac {d}{dt}}\left({\boldsymbol {F}}^{{-1}}\cdot {\boldsymbol {\tau }}\cdot {\boldsymbol {F}}^{{-T}}\right)\right]\cdot {\boldsymbol {F}}^{T}={\mathcal {L}}_{\varphi }[{\boldsymbol {\tau }}]](/2014-wikipedia_en_all_02_2014/I/media/b/f/6/1/bf6168bf4e5feb007a58e3080a11059b.png)
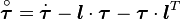

![{\overset {\circ }{{\boldsymbol {\sigma }}}}={\boldsymbol {R}}\cdot \left[{\cfrac {d}{dt}}\left({\boldsymbol {R}}^{{-1}}\cdot {\boldsymbol {\sigma }}\cdot {\boldsymbol {R}}^{{-T}}\right)\right]\cdot {\boldsymbol {R}}^{T}={\boldsymbol {R}}\cdot \left[{\cfrac {d}{dt}}\left({\boldsymbol {R}}^{T}\cdot {\boldsymbol {\sigma }}\cdot {\boldsymbol {R}}\right)\right]\cdot {\boldsymbol {R}}^{T}](/2014-wikipedia_en_all_02_2014/I/media/2/9/5/1/29519b9f4e157d2ad6adcb97e45e391e.png)
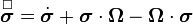
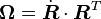 .
.



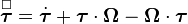

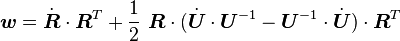
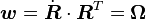
![{\boldsymbol {U}}=\left[{\begin{array}{ccc}\lambda _{{X}}\\&\lambda _{{Y}}\\&&\lambda _{{Z}}\end{array}}\right]](/2014-wikipedia_en_all_02_2014/I/media/8/7/4/7/874701efc58788aeb0e2f70a165a0e2b.png)
![{\dot {{\boldsymbol {U}}}}=\left[{\begin{array}{ccc}{\dot {\lambda }}_{{X}}\\&{\dot {\lambda }}_{{Y}}\\&&{\dot {\lambda }}_{{Z}}\end{array}}\right]](/2014-wikipedia_en_all_02_2014/I/media/d/e/5/9/de5930fea337ca35fb1652da19c9b367.png)
![{\dot {{\boldsymbol {U}}}}\cdot {\boldsymbol {U}}^{{-1}}=\left[{\begin{array}{ccc}{\dot {\lambda }}_{{X}}/\lambda _{{X}}\\&{\dot {\lambda }}_{{Y}}/\lambda _{{Y}}\\&&{\dot {\lambda }}_{{Z}}/\lambda _{{Z}}\end{array}}\right]=U^{{-1}}{\dot {U}}](/2014-wikipedia_en_all_02_2014/I/media/b/1/6/a/b16adb519bf459c26f756eea320803f5.png)
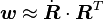
![{\overset {\triangledown }{{\boldsymbol {\sigma }}}}={\mathcal {L}}_{\varphi }[{\boldsymbol {\sigma }}]={\boldsymbol {F}}\cdot \left[{\cfrac {d}{dt}}\left({\boldsymbol {F}}^{{-1}}\cdot {\boldsymbol {\sigma }}\cdot {\boldsymbol {F}}^{{-T}}\right)\right]\cdot {\boldsymbol {F}}^{T}](/2014-wikipedia_en_all_02_2014/I/media/1/9/0/1/190113fc2e8a206ce55934ba8e61b571.png)
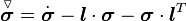
![{\overset {\diamond }{{\boldsymbol {\sigma }}}}={\boldsymbol {F}}^{{-T}}\cdot \left[{\cfrac {d}{dt}}\left({\boldsymbol {F}}^{T}\cdot {\boldsymbol {\sigma }}\cdot {\boldsymbol {F}}\right)\right]\cdot {\boldsymbol {F}}^{{-1}}](/2014-wikipedia_en_all_02_2014/I/media/6/f/9/2/6f926c542f03752829afdeb56136f6e7.png)
