Numerical range

From Wikipedia, the free encyclopedia

In the mathematical field of linear algebra and convex analysis, the numerical range or field of values of a complex n × n matrix A is the set

W(A)=\left\{{\frac {{\mathbf {x}}^{*}A{\mathbf {x}}}{{\mathbf {x}}^{*}{\mathbf {x}}}}\mid {\mathbf {x}}\in {\mathbb {C}}^{n},\ x\not =0\right\}

where x* denotes the Hermitian adjoint of the vector x.

In engineering, numerical ranges are used as a rough estimate of eigenvalues of A. Recently, generalizations of numerical range are used to study quantum computing.

A related concept is the numerical radius, which is the largest absolute values of the numbers in the numerical range, i.e.

r(A)=\sup\{|\lambda |:\lambda \in W(A)\}=\sup _{{\|x\|=1}}|\langle Ax,x\rangle |.

r(A) is a norm.

Properties

  1. The numerical range is the range of the Rayleigh quotient.
  2. (Hausdorff–Toeplitz theorem) The numerical range is convex and compact.
  3. W(\alpha A+\beta I)=\alpha W(A)+\{\beta \} for all square matrix A and complex numbers α and β. Here I is the identity matrix.
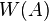  4. W(A) is a subset of the closed right half-plane if and only if A+A^{*} is positive semidefinite.
  5. The numerical range W(\cdot ) is the only function on the set of square matrices that satisfies (2), (3) and (4).
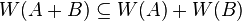  6. (Sub-additive) W(A+B)\subseteq W(A)+W(B).
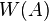  7. W(A) contains all the eigenvalues of A.
  8. The numerical range of a 2×2 matrix is an elliptical disk.
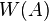  9. W(A) is a real line segment [α, β] if and only if A is a Hermitian matrix with its smallest and the largest eigenvalues being α and β
  10. If A is a normal matrix then 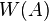W(A) is the convex hull of its eigenvalues.
  11. If α is a sharp point on the boundary of 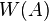W(A), then α is a normal eigenvalue of A.
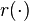  12. r(\cdot ) is a norm on the space of n×n matrices.
  13. r(A^{n})\leq r(A)^{n}

Generalisations

See also


References

    Bibliography
    • Choi, M.D.; Dribs, D.W.; Życzkowski (2006), "Quantum error correcting codes from the compression formalism", Rep. Math. Phys., 58, 2006 .
    • Dirr, G.; Helmkel, U.; Kleinsteuber, M.; Schulte-Herbrüggen, Th. (2006), "A new type of C-numerical range arising in quantum computing", Proc. Appl. Math. Mech. 6, 711–712 (2006) .
    • Bonsall, F.F.; Duncan, J. (1971), Numerical Ranges of Operators on Normed Spaces and of Elements of Normed Algebras, Cambridge University Press, ISBN 978-0-521-07988-4 .
    • Bonsall, F.F.; Duncan, J. (1971), Numerical Ranges II, Cambridge University Press, ISBN 978-0-521-20227-2 Check |isbn= value (help) .
    • Horn, Roger A.; Johnson, Charles R. (1991), Topics in Matrix Analysis, Cambridge University Press, ISBN 978-0-521-46713-1 .
    • Li, C.K. (1996), "A simple proof of the elliptical range theorem", Proc. Am. Math. Soc. 124, 1985 .
    • Keeler, Dennis S.; Rodman, Leiba; Spitkovsky, Ilya M. (1997), "The numerical range of 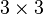3\times 3 matrices", Linear Algebra Applications 252, 115 .
    • Roger A. Horn and Charles R. Johnson, Topics in Matrix Analysis, Chapter 1, Cambridge University Press, 1991. ISBN 0-521-30587-X (hardback), ISBN 0-521-46713-6 (paperback).
    • "Functional Characterizations of the Field of Values and the Convex Hull of the Spectrum", Charles R. Johnson, Proceedings of the American Mathematical Society, 61(2):201-204, Dec 1976.


    This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.