Number density

From Wikipedia, the free encyclopedia

In physics, astronomy, chemistry, biology and geography number density (symbol: n) is an intensive quantity used to describe the degree of concentration of countable objects (particles, molecules, phonons, cells, galaxies, etc.) in physical space: three-dimensional volume number density, two-dimensional area number density, or one-dimensional line number density. Population density is an example of areal number density. The term number concentration (symbol: C) is sometimes used in chemistry for the same quantity, particularly when comparing with other concentrations.

Definition

Volume number density is the number of specified objects per unit volume:^[1]

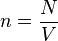$n={\frac {N}{V}}$ ,

where

N is the total number of objects in a volume V.

Here it is assumed^[2] that N is large enough that rounding of the count to the nearest integer does not introduce much of an error, however V is chosen to be small enough that the resulting n does not depend much on the size or shape of the volume V.

Units

In SI system of units, number density is measured in m⁻³, although cm⁻³ is often used. However, these units are not quite practical when dealing with atoms or molecules of gases, liquids or solids at room temperature and atmospheric pressure, because the resulting numbers are extremely large (on the order of 10²⁰). Using the number density of an ideal gas at 0 °C and 1 atm as a yardstick: 1 amagat = 2.6867774×10²⁵ m⁻³ is often introduced as a unit of number density, for any substances at any conditions (not necessarily limited to an ideal gas at 0 °C and 1 atm).^[3]

Usage

Using the number density as a function of spatial coordinates, the total number of objects N in the entire volume V can be calculated as

$N=\iiint _{V}n(x,y,z)\;dV$ ,

where

$dV=dx\,dy\,dz$ is a volume element. If each object possesses the same mass m₀, the total mass m of all the objects in the volume V can be expressed as

$m=\iiint _{V}m_{0}\,n(x,y,z)\;dV$ .

Similar expressions are valid for electric charge or any other extensive quantity associated with countable objects. For example, replacing 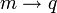$m\rightarrow q$ (total charge) and $m_{0}\rightarrow q_{0}$ (charge of each object) in the above equation will lead to a correct expression for charge.

The number density of solute molecules in a solvent is sometimes called concentration, although usually concentration is expressed as a number of moles per unit volume (and thus called molar concentration).

Relation to other quantities

Molar concentration

For any substance, the number density n (in units of m⁻³) can be expressed in terms of its molar concentration c (in units of mole/m³) as:

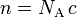$n=N_{{{\rm {A}}}}\,c$ ,

where N_A is the Avogadro constant ≈ 6.022×10²³ mol⁻¹. This is still true if the spatial dimension unit, metre, in both n and c is consistently replaced by any other spatial dimension unit, e.g. if n is in units of cm⁻³ and c is in units of mole/cm³, or if n is in units of L⁻¹ and c is in units of mole/L, etc.

Mass density

For atoms or molecules of a well-defined molecular mass M (in units of kg/mole), the number density can be expressed in terms of the mass density of a substance ρ (in units of kg/m³) as

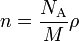$n={\frac {N_{{{\rm {A}}}}}{M}}\rho$ .

Note that the ratio M/N_A is the mass of a single atom or molecule in units of kg.

Examples

The following table lists common examples of number densities at 1 atm and 20 °C, unless otherwise noted.

Molecular^[4] number density and related parameters of some materials
Material	Number density (n)		Molar concentration (c)	Density ( $\rho$ )	Molar mass (M)
Units	(10²⁷ m⁻³) or (10²¹ cm⁻³)	(amagat)	(10³ mol/m³) or (mol/L)	(10³ kg/m³) or (g/cm³)	(10⁻³ kg/mol) or (g/mol)
ideal gas	0.02504	0.932	0.04158	41.58×10⁻⁶×M	M
dry air	0.02504	0.932	0.04158	1.2041×10⁻³	28.9644
water	33.3679	1241.93	55.4086	0.99820	18.01524
diamond	176.2	6556	292.5	3.513	12.01

References and notes

↑ IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (1997). Online corrected version: (2006–) "number concentration".
↑ Clayton T. Crowe; Martin Sommerfeld; Yutaka Tsuji (1998), Multiphase flows with droplets and particles: allelochemical interactions, CRC Press, p. 18, ISBN 0-8493-9469-4
↑ Joseph Kestin (1979), A Course in Thermodynamics 2, Taylor & Francis, p. 230, ISBN 0-89116-641-6
↑ For elemental substances, atomic densities/concentrations are used

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.