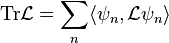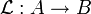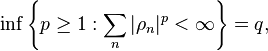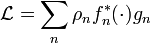Nuclear operator

From Wikipedia, the free encyclopedia

In mathematics, a nuclear operator is a compact operator for which a trace may be defined, such that the trace is finite and independent of the choice of basis (at least on well behaved spaces; there are some spaces on which nuclear operators do not have a trace). Nuclear operators are essentially the same as trace class operators, though most authors reserve the term "trace class operator" for the special case of nuclear operators on Hilbert spaces. The general definition for Banach spaces was given by Grothendieck. This article concentrates on the general case of nuclear operators on Banach spaces; for the important special case of nuclear (=trace class) operators on Hilbert space see the article on trace class operators.

Compact operator

An operator ${\mathcal {L}}$ on a Hilbert space ${\mathcal {H}}$

${\mathcal {L}}:{\mathcal {H}}\to {\mathcal {H}}$

is said to be a compact operator if it can be written in the form^{[citation needed]}

${\mathcal {L}}=\sum _{{n=1}}^{N}\rho _{n}\langle f_{n},\cdot \rangle g_{n}$

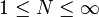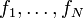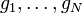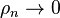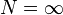where $1\leq N\leq \infty$ and $f_{1},\ldots ,f_{N}$ and $g_{1},\ldots ,g_{N}$ are (not necessarily complete) orthonormal sets. Here, $\rho _{1},\ldots ,\rho _{N}$ are a set of real numbers, the singular values of the operator, obeying $\rho _{n}\to 0$ if $N=\infty$ . The bracket $\langle \cdot ,\cdot \rangle$ is the scalar product on the Hilbert space; the sum on the right hand side must converge in norm.

Nuclear operator

An operator that is compact as defined above is said to be nuclear or trace-class if

$\sum _{{n=1}}^{\infty }|\rho _{n}|<\infty$

Properties

A nuclear operator on a Hilbert space has the important property that its trace may be defined so that it is finite and is independent of the basis. Given any orthonormal basis 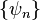$\{\psi _{n}\}$ for the Hilbert space, one may define the trace as

${\mbox{Tr}}{\mathcal {L}}=\sum _{n}\langle \psi _{n},{\mathcal {L}}\psi _{n}\rangle$

since the sum converges absolutely and is independent of the basis^{[citation needed]}. Furthermore, this trace is identical to the sum over the eigenvalues of ${\mathcal {L}}$ (counted with multiplicity).

On Banach spaces

See main article Fredholm kernel.

The definition of trace-class operator was extended to Banach spaces by Alexander Grothendieck in 1955.

Let A and B be Banach spaces, and A' be the dual of A, that is, the set of all continuous or (equivalently) bounded linear functionals on A with the usual norm. Then an operator

${\mathcal {L}}:A\to B$

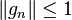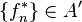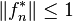is said to be nuclear of order q if there exist sequences of vectors $\{g_{n}\}\in B$ with $\Vert g_{n}\Vert \leq 1$ , functionals $\{f_{n}^{*}\}\in A'$ with $\Vert f_{n}^{*}\Vert \leq 1$ and complex numbers $\{\rho _{n}\}$ with

$\inf \left\{p\geq 1:\sum _{n}|\rho _{n}|^{p}<\infty \right\}=q,$

such that the operator may be written as

${\mathcal {L}}=\sum _{n}\rho _{n}f_{n}^{*}(\cdot )g_{n}$

with the sum converging in the operator norm.

With additional steps, a trace may be defined for such operators when A = B.

Operators that are nuclear of order 1 are called nuclear operators: these are the ones for which the series ∑ρ_n is absolutely convergent. Nuclear operators of order 2 are called Hilbert-Schmidt operators.

More generally, an operator from a locally convex topological vector space A to a Banach space B is called nuclear if it satisfies the condition above with all f_n^* bounded by 1 on some fixed neighborhood of 0 and all g_n bounded by 1 on some fixed neighborhood of 0.

References

A. Grothendieck (1955), Produits tensoriels topologiques et espace nucléaires,Mem. Am. Math.Soc. 16. MR 0075539
A. Grothendieck (1956), La theorie de Fredholm, Bull. Soc. Math. France, 84:319-384. MR 0088665
A. Hinrichs and A. Pietsch (2010), p-nuclear operators in the sense of Grothendieck, Mathematische Nachrichen 283: 232-261. doi:10.1002/mana.200910128 MR 2604120
G. L. Litvinov (2001), "Nuclear operator", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4

v t e Functional analysis

Local Notions on Sets	Absolutely convex Absorbing Balanced Bounded Cones (Linear, Convex cone) Convex Radial Star-shaped Symmetric

Types of TVSs	Banach Barrelled Bornological Brauner F-space Finite-dimensional Fréchet (Tame) Hilbert LF Locally convex Mackey Montel Nuclear Normed (Norm) Reflexive Riesz Smith Stereotype Topological tensor product (of Hilbert spaces) Webbed

Spaces of Maps	Dual space Dual topology Operator topologies Strong Topology (Polar, Operator) Topology of uniform convergence Weak topology (operator) Ultrastrong topology Ultraweak topology

Types of Linear operators	Adjoint Bilinear (form) Bounded (Unbounded) Closed Continuous (Discontinuous) Compact Fredholm Hilbert–Schmidt Functionals (Positive) Normal Nuclear Self-adjoint Strictly singular Trace class Transpose Unitary

Operations on Sets	Algebraic interior (core) Interior Minkowski addition Polar

Banach Algebras	C-algebras Spectrum (of a C-algebra, Spectral radius) Spectral theory

Important Theorems	Banach–Alaoglu Banach–Saks Banach–Mazur Bessel's inequality Cauchy–Schwarz inequality Closed range Closed graph Eberlein–Šmulian Freudenthal spectral Gelfand–Mazur Goldstine Hahn–Banach (Hyperplane separation) Kakutani fixed-point Lomonosov's Invariant Subspace Mackey–Arens Mazur's lemma M. Riesz extension Open mapping Parseval's identity Schauder fixed-point

Analysis	Bochner space Derivatives (Fréchet derivative, Gâteaux derivative, Functional, Holomorphy) Differentiation in Fréchet spaces Integrals (Bochner, Dunford, Gelfand–Pettis, Regulated, Weak) Functional calculus Inverse function theorem (Nash–Moser theorem) Vector measure

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.