Novikov ring

From Wikipedia, the free encyclopedia

For a concept in quantum cohomology, see the linked article.

In mathematics, given an additive subgroup $\Gamma \subset {\mathbb {R}}$ , the Novikov ring $\operatorname {Nov}(\Gamma )$ of $\Gamma$ is the subring of ${\mathbb {Z}}[\![\Gamma ]\!]$ consisting of formal power series 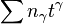$\sum n_{\gamma }t^{\gamma }$ such that 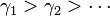$\gamma _{1}>\gamma _{2}>\cdots$ and $\gamma _{i}\to -\infty$ . The notion was introduced by S. P. Novikov in the papers that initiated the generalization of Morse theory using a closed one-form instead of a function.

The Novikov ring $\operatorname {Nov}(\Gamma )$ is a principal ideal domain.

References

Farber, Michael (2004). Topology of closed one-forms. Mathematical surveys and monographs 108. American Mathematical Society. ISBN 0-8218-3531-9. Zbl 1052.58016.
S. P. Novikov, Multi-valued functions and functionals: An analogue of Morse theory. Soviet Math. Doklady 24 (1981), 222–226.
S. P. Novikov: The Hamiltonian formalism and a multi-valued analogue of Morse theory. Russian Mathematical Surveys 35:5 (1982), 1–56.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.