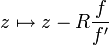Nova fractal
From Wikipedia, the free encyclopedia

A PhonexDoubleNova fractal, rendered using five layers in UltraFractal.

A nova fractal with Re(R) = 1.0, and z0 = c.

A nova fractal with Re(R) = 2.0, and z0 = c.

A nova fractal with Re(R) = 3.0, and z0 = c.

A 129804.49 times magnification at the point (-0.43608549343268, -0.102470623996602) on the novaMandelbrot fractal with start value 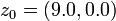 , exponent
, exponent 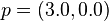 and relaxation
and relaxation  .
.
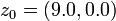 , exponent
, exponent 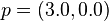 and relaxation
and relaxation  .
.Nova fractal is a family of fractals related to the Newton fractal. Nova is a formula that is implemented in most[citation needed] fractal art software.
Formula
The formula for the Nova fractal[citation needed] is a generalization of a Newton fractal:
where  is said to be a relaxation constant and
is said to be a relaxation constant and 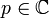 . If c = 0, this expression reduces to the Newton fractal formula:
. If c = 0, this expression reduces to the Newton fractal formula:
for 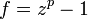 . Usually,
. Usually,  is assigned the value 3, while
is assigned the value 3, while  is an adjustable parameter, and
is an adjustable parameter, and  is the location variable, for a "Mandelbrot Nova".
is the location variable, for a "Mandelbrot Nova".
| ||||||||||||||||||||||||||||
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.