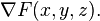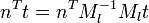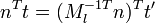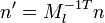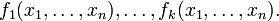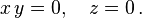Normal (geometry)


In geometry, a normal is an object such as a line or vector that is perpendicular to a given object. For example, in the two-dimensional case, the normal line to a curve at a given point is the line perpendicular to the tangent line to the curve at the point.
In the three-dimensional case a surface normal, or simply normal, to a surface at a point P is a vector that is perpendicular to the tangent plane to that surface at P. The word "normal" is also used as an adjective: a line normal to a plane, the normal component of a force, the normal vector, etc. The concept of normality generalizes to orthogonality.
The concept has been generalized to differentiable manifolds of arbitrary dimension embedded in a Euclidean space. The normal vector space or normal space of a manifold at a point P is the set of the vectors which are orthogonal to the tangent space at P. In the case of differential curves, the curvature vector is a normal vector of special interest.
The normal is often used in computer graphics to determine a surface's orientation toward a light source for flat shading, or the orientation of each of the corners (vertices) to mimic a curved surface with Phong shading.
Normal to surfaces in 3D space
Calculating a surface normal
For a convex polygon (such as a triangle), a surface normal can be calculated as the vector cross product of two (non-parallel) edges of the polygon.
For a plane given by the equation 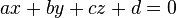 , the vector
, the vector 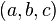 is a normal.
is a normal.
For a plane given by the equation
-
 ,
,
i.e., a is a point on the plane and b and c are (non-parallel) vectors lying on the plane, the normal to the plane is a vector normal to both b and c which can be found as the cross product 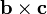 .
.
For a hyperplane in n+1 dimensions, given by the equation
 ,
,
where a0 is a point on the hyperplane and ai for i = 1, ..., n are non-parallel vectors lying on the hyperplane, a normal to the hyperplane is any vector in the null space of A where A is given by
-
![A=[{\mathbf {a}}_{1}\dots {\mathbf {a}}_{n}]](/2014-wikipedia_en_all_02_2014/I/media/b/9/1/e/b91e15da43124f4681f973a6ddd8fb3a.png) .
.
That is, any vector orthogonal to all in-plane vectors is by definition a surface normal.
If a (possibly non-flat) surface S is parameterized by a system of curvilinear coordinates x(s, t), with s and t real variables, then a normal is given by the cross product of the partial derivatives
If a surface S is given implicitly as the set of points  satisfying
satisfying 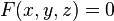 , then, a normal at a point
, then, a normal at a point  on the surface is given by the gradient
on the surface is given by the gradient
since the gradient at any point is perpendicular to the level set, and 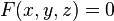 (the surface) is a level set of
(the surface) is a level set of  .
.
For a surface S given explicitly as a function  of the independent variables
of the independent variables 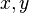 (e.g.,
(e.g., 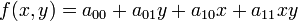 ), its normal can be found in at least two equivalent ways.
The first one is obtaining its implicit form
), its normal can be found in at least two equivalent ways.
The first one is obtaining its implicit form 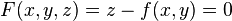 , from which the normal follows readily as the gradient
, from which the normal follows readily as the gradient
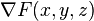 .
.
(Notice that the implicit form could be defined alternatively as
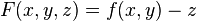 ;
;
these two forms correspond to the interpretation of the surface being oriented upwards or downwards, respectively, as a consequence of the difference in the sign of the partial derivative 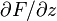 .)
The second way of obtaining the normal follows directly from the gradient of the explicit form,
.)
The second way of obtaining the normal follows directly from the gradient of the explicit form,
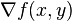 ;
;
by inspection,
-
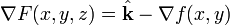 , where
, where 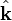 is the upward unit vector.
is the upward unit vector.
Note that this is equal to 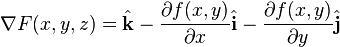 , where
, where  and
and  are the x and y unit vectors.
are the x and y unit vectors.
If a surface does not have a tangent plane at a point, it does not have a normal at that point either. For example, a cone does not have a normal at its tip nor does it have a normal along the edge of its base. However, the normal to the cone is defined almost everywhere. In general, it is possible to define a normal almost everywhere for a surface that is Lipschitz continuous.
Uniqueness of the normal

A normal to a surface does not have a unique direction; the vector pointing in the opposite direction of a surface normal is also a surface normal. For a surface which is the topological boundary of a set in three dimensions, one can distinguish between the inward-pointing normal and outer-pointing normal, which can help define the normal in a unique way. For an oriented surface, the surface normal is usually determined by the right-hand rule. If the normal is constructed as the cross product of tangent vectors (as described in the text above), it is a pseudovector.
Transforming normals
When applying a transform to a surface it is sometimes convenient to derive normals for the resulting surface from the original normals. All points P on tangent plane are transformed to P′. We want to find n′ perpendicular to P. Let t be a vector on the tangent plane and Ml be the upper 3x3 matrix (translation part of transformation does not apply to normal or tangent vectors).
So use the inverse transpose of the linear transformation (the upper 3x3 matrix) when transforming surface normals. Also note that the inverse transpose is equal to the original matrix if the matrix is orthonormal, i.e. purely rotational with no scaling or shearing.
Hypersurfaces in n-dimensional space
The definition of a normal to a surface in three-dimensional space can be extended to  -dimensional hypersurfaces in a
-dimensional hypersurfaces in a  -dimensional space. A hypersurface may be locally defined implicitly as the set of points
-dimensional space. A hypersurface may be locally defined implicitly as the set of points  satisfying an equation
satisfying an equation  , where
, where  is a given scalar function. If
is a given scalar function. If  is continuously differentiable then the hypersurface is a differentiable manifold in the neighbourhood of the points where the gradient is not null. At these points the normal vector space has dimension one and is generated by the gradient
is continuously differentiable then the hypersurface is a differentiable manifold in the neighbourhood of the points where the gradient is not null. At these points the normal vector space has dimension one and is generated by the gradient
The normal line at a point of the hypersurface is defined only if the gradient is not null. It is the line passing through the point and having the gradient as direction.
Varieties defined by implicit equations in n-dimensional space
A differential variety defined by implicit equations in the n-dimensional space is the set of the common zeros of a finite set of differential functions in n variables
The Jacobian matrix of the variety is the k×n matrix whose i-th row is the gradient of fi. By implicit function theorem, the variety is a manifold in the neighborhood of a point of it where the Jacobian matrix has rank k. At such a point P, the normal vector space is the vector space generated by the values at P of the gradient vectors of the fi.
In other words, a variety is defined as the intersection of k hypersurfaces, and the normal vector space at a point is the vector space generated by the normal vectors of the hypersurfaces at the point.
The normal (affine) space at a point P of the variety is the affine subspace passing through P and generated by the normal vector space at P.
These definitions may be extended verbatim to the points where the variety is not a manifold.
Example
Let V be the variety defined in the 3-dimensional space by the equations
This variety is the union of the x-axis and the y-axis.
At a point (a, 0, 0) where a≠0, the rows of the Jacobian matrix are (0, 0, 1) and (0, a, 0). Thus the normal affine space is the plane of equation x=a. Similarly, if b≠0, the normal plane at (0, b, 0) is the plane of equation y=b.
At the point (0, 0, 0) the rows of the Jacobian matrix are (0, 0, 1) and (0,0,0). Thus the normal vector space and the normal affine space have dimension 1 and the normal affine space is the z-axis.
Uses
- Surface normals are essential in defining surface integrals of vector fields.
- Surface normals are commonly used in 3D computer graphics for lighting calculations; see Lambert's cosine law.
- Surface normals are often adjusted in 3D computer graphics by normal mapping.
- Render layers containing surface normal information may be used in Digital compositing to change the apparent lighting of rendered elements.
Normal in geometric optics

The normal is the line perpendicular to the surface[1] of an optical medium. In reflection of light, the angle of incidence and the angle of reflection are respectively the angle between the normal and the incident ray and the angle between the normal and the reflected ray.
See also
References
- ↑ "The Law of Reflection". The Physics Classroom Tutorial. Retrieved 2008-03-31.
External links
- An explanation of normal vectors from Microsoft's MSDN
- Clear pseudocode for calculating a surface normal from either a triangle or polygon.