Nonlinear expectation

From Wikipedia, the free encyclopedia

In probability theory, a nonlinear expectation is a nonlinear generalization of the expectation. Nonlinear expectations are useful in utility theory as they more closely match human behavior than traditional expectations.^{[citation needed]}

Definition

A functional ${\mathbb {E}}:{\mathcal {H}}\to {\mathbb {R}}$ (where ${\mathcal {H}}$ is a vector lattice on a probability space) is a nonlinear expectation if it satisfies:^[1]^[2]

Monotonicity: if $X,Y\in {\mathcal {H}}$ such that $X\geq Y$ then ${\mathbb {E}}[X]\geq {\mathbb {E}}[Y]$
Preserving of constants: if 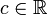$c\in {\mathbb {R}}$ then ${\mathbb {E}}[c]=c$

Often other properties are also desirable, for instance convexity, subadditivity, positive homogeneity, and translative of constants.^[1]

Examples

Expected value
Choquet expectation
g-expectation
If $\rho$ is a risk measure then ${\mathbb {E}}[X]:=\rho (-X)$ defines a nonlinear expectation

References

↑ 1.0 1.1 Shige Peng (2006). "G–Expectation, G–Brownian Motion and Related Stochastic Calculus of Itô Type" (pdf). Abel Symposia (Springer-Verlag) 2. Retrieved August 9, 2012.
↑ Peng, S. (2004). "Nonlinear Expectations, Nonlinear Evaluations and Risk Measures" (pdf). Stochastic Methods in Finance. Lecture Notes in Mathematics 1856. pp. 165–138. doi:10.1007/978-3-540-44644-6_4. ISBN 978-3-540-22953-7. Retrieved August 9, 2012.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.