Noncommutative topology
Noncommutative topology in mathematics is a term applied to the strictly C*-algebraic part of the noncommutative geometry program. The program has its origins in the Gel'fand duality between the topology of locally compact spaces and the algebraic structure of commutative C*-algebras.
Several topological properties can be formulated as properties for the C*-algebras without making reference to commutativity or the underlying space, and so have an immediate generalization.
Amongst these are compactness (being unital), dimension (real or stable rank), connectedness (projectionless algebra) and K-theory. So we think of a noncommutative C*-algebra as the algebra of functions on a 'noncommutative space' which does not exist classically.
A major tool in the field is a bivariant version of K-theory called KK-theory. It has a composition product
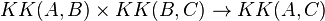
of which the ring structure in ordinary K-theory is a special case. The product gives the structure of a category to KK. It has been related to correspondences of algebraic varieties.[1]